Лінійна алгебра

Теоретичні питання

1. Матриця та її визначник. Методи обчислення визначників п -го порядку. Лінійні операції над матрицями. Множення матриць. Обернена матриця.

2. Означення та властивості лінійного простору. Базис і розмірність лінійного простору. Ізоморфізм лінійних просторів. Підпростори та лінійні оболонки. Ранг матриці, його знаходження.

3. Поняття системи лінійних рівнянь та її розв¢язку, умова сумісності. Знаходження розв¢язків квадратної системи лінійних рівнянь з 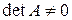. Знаходження всіх розв¢язків загальної системи лінійних рівнянь.

4. Однорідні системи лінійних рівнянь. Зв¢язок між розв¢язками неоднорідної лінійної системи і відповідної їй однорідної системи.

5. Поняття та властивості евклідового простору. Ортонормований базис, його властивості. Ізоморфізм евклідових просторів.

6. Означення лінійного оператора. Дії над лінійними операторами, властивості. Матричний запис лінійних операторів. Відповідність між діями над лінійними операторами та над матрицями.

7. Перетворення матриці лінійного оператора при переході до нового базису. Характеристичний многочлен лінійного оператора. Власні значення та власні елементи лінійного оператора.

8. Лінійні оператори в евклідовому просторі. Спряжені та самоспряжені оператори. Основні властивості самоспряжених операторів.

9. Білінійні та квадратичні форми. Перетворення матриці білінійної форми при переході до нового базису. Зведення квадратичної форми до канонічного вигляду. Білінійні та квадратичні форми в евклідовому просторі.

10. Застосування теорії квадратичних форм до дослідження алгебраїчних рівнянь другого степеня. Зведення загального рівняння лінії другого порядку до канонічного вигляду.

Date: 2015-04-23; view: 477; Нарушение авторских прав