Основы симплекс-метода

Рассмотрим задачу линейного программирования с условиями в форме равенств, которые задают выпуклое множество (многогранник) допустимых решений.

Прямой перебор вершин выпуклого многогранника ограничений является трудоемким способом решения ЗЛП. Поэтому разработаны и разрабатываются алгоритмы направленного поиска оптимального решения. Наиболее распространенным методом поиска является симплекс-метод (метод последовательного улучшения плана). При использовании этого метода решение задачи распадается на два этапа:

1) отыскание координат первой вершины многогранника ограничений, или, в терминах линейного программирования, опорного решения (опорного плана, базисного решения);

2) отыскание координат вершины многогранника ограничений, соответствующей оптимальному значению (оптимального плана).

Таким образом, при использовании симплекс-метода вначале находят произвольную вершину многогранника, т.е. опорное решение 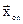,определяют значение целевой функции в опорной вершине 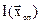. Затем находят ребро многогранника ограничений, вдоль которого целевая функция наиболее быстро растет (если определяется максимум функции) или убывает (если отыскивается минимум), и находят следующую вершину многогранника ограничений вдоль этого ребра. Новую вершину принимают за опорную и всю процедуру повторяют, т.е.

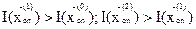и т. д.

Поиск заканчивают, когда приходят в вершину, для которой не найдется ни одного смежного ребра, вдоль которого будет возрастать (или убывать при поиске минимума), т.е. в точке оптимума будет ухудшаться при движении во всех допустимых направлениях.

Симплекс-метод позволяет найти крайнюю точку области допустимых решений и определить является ли она точкой экстремума функции .

Рассмотрим вычислительный аспект симплекс-метода.

Симплекс-метод является универсальным в том смысле, что позволяет решать задачу в общей постановке, хотя требует приведения ее к определенному (стандартному) виду:

Найти 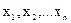доставляющие минимум функции

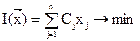(4.15)

при условиях

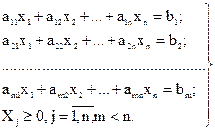(4.16)

При m<n существует множество решений и это множество решений может быть представлено как

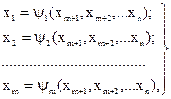(4.17)

где 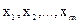– базисные переменные;

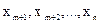-свободные переменные;

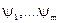-линейные функции свободных переменных.

Вследствие линейности функций 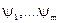равенства (4.14) могут быть приведены к виду

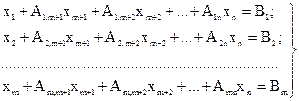(4.18)

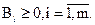(4.19)

Здесь коэффициенты 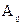и свободные члены 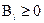определяются величинам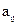и и 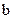, входящими в уравнения (4.16).

Системе уравнений (4.16) присуща следующая особенность: переменная 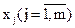входит только в уравнение с номером i=j, имея при этом коэффициент, равный единице, и не входят в остальные m-1 уравнений, для которых .

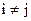Такая система называется канонической. Основным ее преимуществом является то, что она позволяет легко указать множество всех возможных решений (4.16), среди которых находятся базисные решения.

Частное решение системы (4.18), получаемое приравниваем свободных переменных к нулю, называется базисным. Оно имеет вид

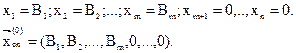(4.20)

При этом 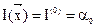. Приведем следующие три утверждения, которые положены в основу построения алгоритма улучшения допустимого базисного решения и решения задачи в целом.

1. Допустимое базисное решение системы уравнений (4.18) соответствует крайней точке области, определяемой системой линейных ограничений.

2. Если ЗЛП имеет оптимальное решение, то существует, по крайней мере, одно базисное оптимальное решение. Теперь симплекс-метод может быть определен как метод, предполагающий последовательный анализ базисных решений системы (4.16).

3. Базисное допустимое решение (4.20) является оптимальным тогда, когда коэффициенты 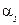при свободных переменных 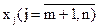в функции (после ее выражения через свободные переменные) неотрицательны.

Таким образом, получен критерий оценки оптимальности решения задачи линейного программирования. Однако, с первой попытки найти такое решение не всегда удается. Даже в тех случаях, когда задача сведена к допустимой канонической форме, очевидное базисное решение (4.20) чаще всего оказывается промежуточным. Поэтому необходимо рассмотреть процесс улучшения решения, заключающийся в поиске нового базисного решения,которому соответствует более близкое к оптимальному значение .

Допустим, что базисное решение (4.20) не является оптимальным, т.е. среди коэффициентов 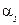в функции 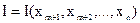есть отрицательные. Чтобы перейти от решения (4.20) к другому базисному решению нужно сделать отличной от нуля (ввести в базис) какую-то из свободных переменных 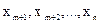, обратив в ноль одну из базисных переменных 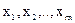. Имея в виду ограничение 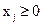, можно сказать, что при таком переходе уменьшится только тогда, когда вводимая в базис переменная будет иметь в выражении отрицательный коэффициент. Естественно, уменьшение будет тем заметнее, чем больше по модулю соответствующий коэффициент .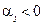

Обозначим через S тот номер j из m+1,…,n, для которого величина 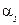отрицательна и максимальна по модулю, т.е. 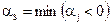. Вводим 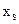в базис и представим базисные переменные и в виде

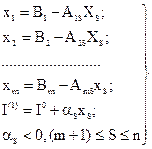(4.21)

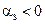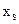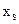Поскольку , нужно как можно больше увеличивать в стремлении минимизировать . Однако возрастание может продолжаться лишь до тех пор, пока какая-то из переменных 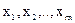не обратится в ноль. Это произойдет, если хотя бы один коэффициент 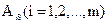в системе уравнений (4.21) положителен (по исходному условию (4.19) все 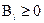). Если же 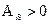для нескольких индексов i из 1,2,…m, то при возрастании 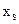в ноль обратится первой та базисная переменная из (4.21), которой отвечает наименьшая величина отношения 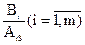. Предположим, что эта переменная есть 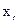,тогда предельное значение 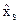, до которого можно увеличить 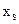,найдется как

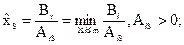(4.22)

.

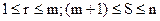При этом 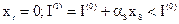, так как 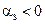, а .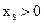

Необходимо подчеркнуть, что равенство нулю хотя бы одного свободного члена 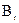при каких-то (случай вырожденного базисного решения, в котором равными нулю оказываются не только свободные переменные, но и некоторые базисные, так как 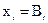) означает невозможность ввода 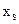в базис с соблюдением условия .

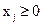Указанная процедура перехода может быть повторена, если новое базисное решение допускает дальнейшее улучшение (уменьшение) значения . Симплекс-алгоритм состоит в последовательном повторении подобных операций до тех пор, пока не будет найдено оптимальное решение ЗЛП.

ЗЛП имеет множество решений, если при достижении оптимальной вершины в выражении функции 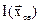будет отсутствовать какая-нибудь из свободных переменных.

Если на каком-то этапе окажется, что все коэффициенты 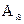отрицательны и увеличение свободной переменной 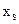не ограничено, (область открытая), то оптимального решения не существует .

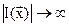Надо отметить, что предусмотренный симплекс-алгоритмом процесс поиска 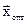закончится на конечном числе шагов, если ни на одном из них не возникнут вырожденные базисные решения.

Симплекс-метод, как указывалось выше, предполагает на первом этапе решения задачи выбор базисных переменных 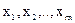таким образом, чтобы выполнялись условия (4.19), что является трудоемкой задачей. Для такого выбора можно вводить дополнительные положительные переменные 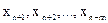.Этот подход позволяет установить существование допустимых решений. Однако для его реализации требуется решать одну вспомогательную задачу линейной оптимизации тем же симплекс-методом.

Рассмотрим исходную задачу (4.15),(4.16). Для нее построим вспомогательную задачу: найти

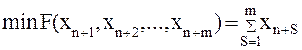(4.23)

для известного вектора 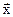с m дополнительными переменными

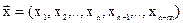
и условиями

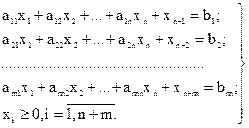(4.24)

Система уравнений (4.24) является канонической системой. Принимая за свободные переменные, а 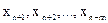- за базисные, получаем базисное допустимое решение вспомогательной задачи:

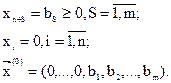
Затем, применяя последовательно шаги симплекс-алгоритма находим оптимальное решение вспомогательной задачи. Если это решение таково, что 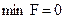,то оно определяет допустимое базисное решение исходной задачи; если 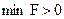, то исходная задача не имеет допустимых решений.

Применение симплекс-метода для решения задач с условиями типа неравенство. Пусть ограничения задаются не уравнениями, а неравенствами. Их число обозначим через d. Неравенства могут быть легко сведены к уравнениям, если ввести в таком же количестве дополнительные положительные переменные. Для неравенства

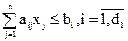
получим

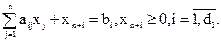
Для неравенства

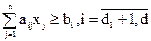
получим

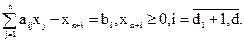
Тогда задача оптимизации может быть записана в следующей форме:

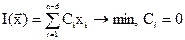при

при условиях

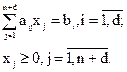
Таким образом, получили ЗЛП с условиями в форме равенств, которая решается симплекс-методом.

ЛИТЕРАТУРА

1. Зайцев М.Г., Варюхин С.В. Методы оптимизации управления и принятия решений.-М.: ДЕЛО, 2007.-684 с.

2. Э. Хофер, Р. Лундерштедт Численные методы оптимизации.- М.:БИНОМ, 1998.-134 с.

3. Александров А.Г. Оптимальные и адаптивные системы.– М.: Высшая школа, 1999.– 263 с.

4. П. В. Конюховский Математические методы исследования операций в эко номике. - М.: ЮНИТИ, 2000.- 205 с.

5. Банди Б. Методы оптимизации. Вводный курс: Перевод с английского.– М.: Радио и связь, 1988.– 128 с.

6. Батищев Д.И. Поисковые методы оптимального проектирования.– М.: ЮНИТИ, 1995.– 216 с.

7. Бояринов А.И., Кафаров В.В. Методы оптимизации в химической технологии.– М.: Химия, 1975.– 576 с.

8. Воронов А.А. Основы теории автоматического управления. Ч.3. Оптимальные, многосвязные и адаптивные системы.– Л.: Энергия, 1980.– 328 с.

9. Дегтярев Ю.И. Методы оптимизации.– М.: ЮНИТИ, 1998.– 272 с.

10. Куропаткин П.В. Оптимальные и адаптивные системы.– М.: Высшая школа, 1990.– 287 с.

11. Понтрягин Л.Г. Математическая теория оптимальных процессов.– М.: Наука, 1976.– 392 с.

12. Растригин Л.А. Системы экстремального управления.– М.: Наука, 1984.– 632 с.

13. Реклейтис Г. Оптимизация в технике: В 2 кн.: Перевод с английского. – М.: Мир, 1996.– 670 с.

14. Ротач В.Я. Теория автоматического управления теплоэнергетическими процессами.– М.: Энергоатомиздат, 1995.– 296с.

15. Уайлд Д.Дж. Методы поиска экстремума: Перевод с английского.– М.: Наука, 1987.– 268 с.

16. Фельдбаум А.А. Основы теории оптимальных автоматических систем.– М.: Наука, 1986.– 624 с.

17. Цирлин А.М. Оптимальное управление технологическими процессами.– М.: Энергоатомиздат, 1996.– 400 с.

18 Ефимова А.Б Сборник задач по математике. Методы оптимизации. - М.: Наука, 1999.-198 с.

СОДЕРЖАНИЕ

........... 1 Методы одномерной оптимизации.............. 3

1.1 Одномерная оптимизация методом

классического анализа.................................. 3

1.2 Метод равномерного поиска................... 5

1.3 Метод поразрядного приближения........ 5

1.1 Метод дихотомии..................................... 6

1.5 Метод золотого сечения.......................... 7

1.6 Метод квадратичной интерполяции........ 8

........... 2 Методы многомерной оптимизации

на основе преобразования задач................. 10

2.1 Метод классического анализа...................... 11

2.2 Метод исключения переменных.............. 13

2.3 Метод множителей Лагранжа.................. 14

2.4 Пример применения метода множителей

Лагранжа....................................................... 16

2.5 Метод множителей Лагранжа с

ограничениями в виде неравенств............... 19

2.6 Экономическая интерпретация

множителей Лагранжа.................................. 21

2.7 Метод штрафных функций...................... 23

........... 3 Поисковые методы многомерной оптимизации 25

3.1 Общие сведения........................................ 25

3.2 Градиентные методы оптимизации......... 29

3.2.1 Метод релаксации................................. 29

3.2.2 Метод градиента................................... 32

3.2.3 Метод наискорейшего спуска............... 35

3.3 Безградиентные методы оптимизации поиска 37

3.3.1 Метод сканирования............................. 38

3.3.2 Метод Гаусса-Зейделя........................... 39

3.3.3 Метод поиска по симплексу.................. 41

........... 4 Линейная оптимизация................................. 46

4.1 Примеры задач линейной оптимизации. 47

4.2 Общая постановка задачи

линейной оптимизации................................. 49

4.3 Геометрическая интерпретация ЗЛП.......... 50

4.4 Основы симплекс-метода............................. 52

СПИСОК ИСПОЛЬЗОВАННЫХ

ИСТОЧНИКОВ.................................................. 59

Date: 2015-05-23; view: 880; Нарушение авторских прав