
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры задач линейной оптимизации
|
|
Транспортная задача. Имеется n поставщиков, производителей k видов продукции. Возможность каждого поставщика характеризуется вектором 
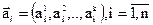 , где
, где 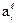 - количество
- количество  -го вида продукции, производимое
-го вида продукции, производимое 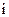 -м поставщиком. Вся производимая продукция распределяется
-м поставщиком. Вся производимая продукция распределяется 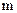 потребителям (заказчикам). Каждый потребитель характеризуется вектором
потребителям (заказчикам). Каждый потребитель характеризуется вектором 
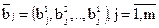 , где
, где 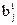 - количество
- количество  -го вида продукции, производимое
-го вида продукции, производимое 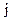 -м заказчиком. Пусть все, что производится поставщиками, потребляется заказчиками. Тогда необходимо выполнение условия
-м заказчиком. Пусть все, что производится поставщиками, потребляется заказчиками. Тогда необходимо выполнение условия
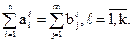 (4.1)
(4.1)
Между поставщиками и потребителями существует транспортная сеть, затраты на перевозки которой характеризуется матрицей стоимости

где 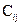 – стоимость перевозки единицы веса продукции от i-го поставщика к
– стоимость перевозки единицы веса продукции от i-го поставщика к 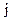 -му заказчику.
-му заказчику.
Необходимо синтезировать план перевозок по каждому виду продукции:
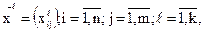
где 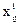 - количество
- количество  -го вида продукции, перевозимое от i-го поставщика к j-му потребителю.
-го вида продукции, перевозимое от i-го поставщика к j-му потребителю.
Этот план должен минимизировать транспортные затраты:
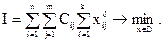 (4.2)
(4.2)
Множество D допустимых решений увязывает количество отправленных и полученных грузов. С учетом условия (4.1) имеем следующие ограничения (множество D):
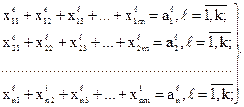 (4.3)
(4.3)
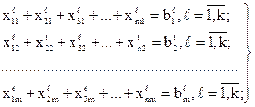 (4.4)
(4.4)
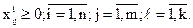 (4.5)
(4.5)
Таким образом, получены 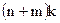 ограничений в форме равенств (4.3), (4.4) и
ограничений в форме равенств (4.3), (4.4) и 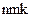 ограничений в форме неравенств (4.5).
ограничений в форме неравенств (4.5).
Эти ограничения можно представить в более компактной форме:
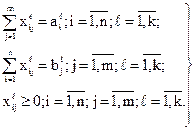 (4.6)
(4.6)
Размерность неизвестного вектора 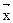 в данной задаче равна
в данной задаче равна 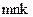 .
.
Таким образом получили линейную целевую функцию (4.2), линейные ограничения (4.6) и, следовательно, задачу линейного программирования.
Задача об оптимальном планировании выпуска продукции. Данная задача об определении максимальной прибыли производства является типичной задачей линейной оптимизации.
Пусть для изготовления n видов продукции в количестве 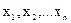 расходуется m видов сырья. Расход сырья i-го вида на единицу j-го вида продукции равен
расходуется m видов сырья. Расход сырья i-го вида на единицу j-го вида продукции равен 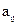 , запас сырья i-го вида ограничен величиной
, запас сырья i-го вида ограничен величиной 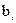 . Каждая единица продукции i-го вида дает прибыль
. Каждая единица продукции i-го вида дает прибыль 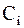 рублей. Задача поиска вектора
рублей. Задача поиска вектора 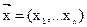 – количества продукции каждого вида, дающего максимальную прибыль, принимает следующую форму: найти
– количества продукции каждого вида, дающего максимальную прибыль, принимает следующую форму: найти 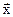 , доставляющий
, доставляющий
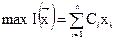
при ограничениях
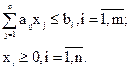
Date: 2015-05-23; view: 776; Нарушение авторских прав