Метод поиска по симплексу

Рассмотрим задачу

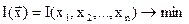. (3.26)

Симплексный метод является безградиентным методом, реализует процедуру прямого поиска оптимума на основе вычисления значения целевой функции. Предполагается, что непрерывна, а 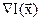может как существовать, так и не существовать, поскольку соответствующие числовые значения не используются. Однако следует отметить, что симплексный метод можно применить для решения задач, в которых 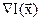существует, но представляет собой сложную векторную функцию управляемых переменных. Наконец, предполагается, что функция унимодальна в рассматриваемой области. Если же метод применяется для анализа мультимодальных функций, то приходится ограничиваться идентификацией локальных оптимумов.

Симплексный метод относится к категории эвристических, которые реализуют процедуры поиска с помощью интуитивных геометрических представлений.

Первые попытки решения оптимизационных без ограничений на основе прямого поиска связаны с использованием процедуры сканирования, что является непригодной для решения задач с числом переменных превышающим 2.

Более полезная идея заключается в выборе базовой точки и оценивания значений в точках, окружающих базовую точку. Например, при решении задач с двумя переменными можно воспользоваться квадратным образцом (рис. 3.12), который является частным случаем кубического образца. В вершинах образца и базовой точке вычисляется значение .

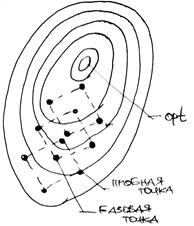
Рисунок 3.13 – Использование квадратного образца для поиска оптимума

Затем «наилучшая» из пяти исследуемых точек выбирается в качестве следующей базовой точки, вокруг которой строится аналогичный образец. Если ни одна из угловых точек не имеет преимущества перед базовой, размеры образца следует уменьшить, после чего продолжить поиск.

Этот тип эволюционной оптимизации был использован Боксом и другими исследователями США для анализа функционирования промышленных предприятий, когда эффект варьирования значений переменных, описывающих производственные процессы, измеряется с ошибкой.

В задачах большой размерности вычисление значений проводится во всех вершинах, а также в центре тяжести гиперкуба (куба в n- мерном пространстве), т. е. в точках так называемого кубического образца. Если количество переменных (размерность пространства, в котором ведётся поиск) равно n, то поиск по кубическому образцу требует 2ⁿ+1 вычислений значения для одного образца. При увеличении и объём вычислений возрастает чрезвычайно быстро. Таким образом, несмотря на логическую простоту поиска по кубическому образцу, возникает необходимость использования более эффективных методов прямого поиска для решения возникающих на практике задач оптимизации.

Одна из вызывающих особый интерес стратегий поиска положена в основу метода поиска по симплексу, предложенного американскими специалистами Спендли, Хекстом и Химсвортом. Следует отметить, что указанный метод не имеет отношения к симплекс-методу линейного программирования, а сходство названий носит случайный характер.

Процедура симплексного поиска базируется на том, что экспериментальным образцом, содержащим наименьшее число точек, является регулярный (правильный) симплекс. Регулярный симплекс в n-мерном пространстве представляет собой многогранник, образованный n+1 равностоящими друг от друга точками – вершинами. Например, в случае двух переменных симплексом является равносторонний треугольник, в трёхмерном пространстве – четырёхгранная пирамида (тетраедр) (рис. 3.13).

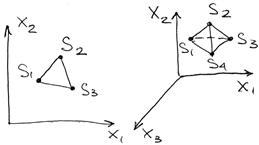
Рисунок 3.14 – Примеры симплекса на плоскости и в пространстве

В алгоритме симплексного используется важное свойство симплексов: против любой из вершин симплекса S_j расположена только одна грань, на которой можно построить новый симплекс путём переноса выбранной вершины на надлежащее расстояние вдоль прямой, проведённой через центр тяжести остальных вершин начального симплекса. Полученная таким образом точка является вершиной нового симплекса, а выбранная при построении вершина начального симплекса исключается (рис. 3.14).

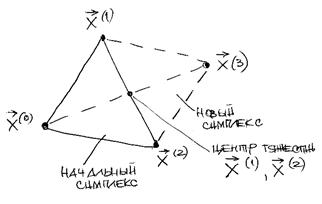
Рисунок 3.15 – Построение нового симплекса на плоскости

Основная идея симплексного метода заключается в том, что по известным значениям в вершинах симплекса находится направление небольшого изменения критерия оптимальности для очередного шага оптимизации.

Рассмотрим алгоритм этого метода на примере отыскания минимума 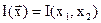функции двух переменных (рис. 3.15).

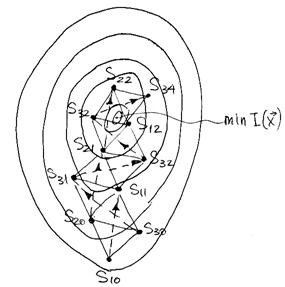
Рисунок 3.16 – Поиск оптимума симплексным методом

Выбирается начальный симплекс S₁₀S₂₀S₃₀ и определяется значение в точках вершин.

По полученным значениям выбирается наихудшая вершина, в которой значение наибольшее (вершина S₁₀). Строится новый симплекс, для чего наихудшая вершина S₁₀ заменяется новой S₁₁, расположенной симметрично относительно центра, находящейся против неё грани. В новой вершине вычисляется значение , которое сравнивается с известными значениями для двух других вершин S₂₀, S₃₀ нового симплекса. Снова находится наихудшая вершина (S₃₀), которая исключается аналогичным образом и т.д.

В результате повторения процедуры исключения наихудшей вершины процесс поиска сходится к оптимальному значению . В районе оптимума может возникнуть циклическое движение по двум или более симплексам, когда вновь полученная вершина окажется наихудшей и её исключение к предыдущему симплексу. На рисунке исключение наихудшей S₃₄ приводит к предыдущей вершине S₃₃, что приводит к зацикливанию алгоритма поиска.

В таких случаях можно воспользоваться следующими правилами:

1) если вершина, которой соответствует наибольшее значение (находится вершина при поиске минимума), построена на предыдущей итерации, то необходимо уменьшить размеры симплекса с помощью коэффициента редукции и построить новый регулярный симплекс, выбрав в качестве базовой точку, которой соответствует наилучшее (минимальное) значение ;

2) построить деформированный симплекс, для чего исключаемая вершина S_j переносится на расстояние 0.5S_jA. При этом происходит сжатие симплекса (рис. 3.16).

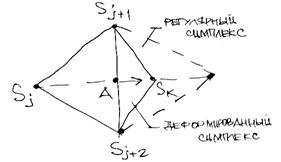
Рисунок 3.17 – Построение деформированного симплекса

Уменьшении размеров симплекса при появлении новых зацикливаний в районе оптимума и продолжают до тех пор, пока не будет достигнута требуемая точность определения оптимума.

Поиск завершается, когда или размеры симплекса, или разности между значениями в вершинах симплекса становятся достаточно малыми.

Реализация алгоритма поиска по симплексу основана на вычислениях двух типов:

1) построение исходного регулярного симплекса при заданных базовой точке и масштабном множителе;

2) расчет координат отражённой вершины.

Построение исходного симплекса. Пусть задана начальная (базовая) точка 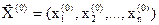и масштабный множитель 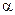. Координаты остальных n вершин симплекса в n-мерном пространстве вычисляются по формуле:

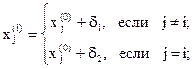
где 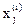– j- ая координата i- ой вершины;

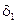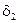, – приращения.

Приращения 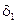, , 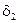зависящие только от n и 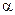, определяются по формулам:

;

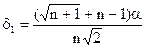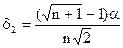
Величина 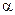выбирается исследователем. При 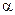=1 рёбра регулярного симплекса имеют единичную длину (длина ребра равна ).

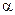Расчёт координат отражённой вершины. Пусть S_L – наихудшая вершина, подлежащая отражению, а 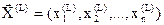– координаты этой вершины. Центр тяжести остальных n вершин (центр противолежащей грани) обозначим A. Тогда координаты точки A вычисляются по приведённым ниже формулам в векторной и скалярной формах соответственно:

; ,

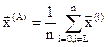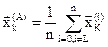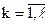
где 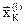– k-ая координата i-ой вершины;

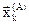– k-ая координата точки A.

Все точки 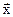прямой, проходящей через точк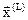и и 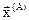, задаются формулой

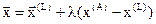, (3.27)

где 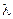-параметр характеризующий расстояние точки на линии от центра.

При 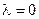получаем исходную точку 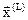; 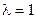соответствует центру тяжести 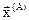. Для того, чтобы построенный симплекс обладал свойством регулярности, отражение должно быть симметричным. Следовательно, новая вершина регулярного симплекса получается при 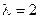. Таким образом, получаем

,

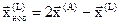где 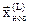– координата отражённой вершины нового симплекса.

При 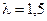получаем деформированный симплекс. При этом исключаемая вершина отражается на расстояние 0.5S_LA от центра A вдоль прямой (6/27).

С учётом этого из уравнения определяем координаты новой вершины деформированного симплекса:

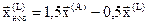
Преимуществами симплексного метода являются:

1) простота расчетов и логической структуры алгоритма, относительно короткая программа для ЭВМ;

2) невысокий уровень требований к объёму памяти ЭВМ, массив данных имеет размерность (n+1, n+2);

3) алгоритм оказывается эффективным даже в тех случаях, когда ошибка вычислений велика, поскольку при его реализации оперируют наибольшими значениями в вершинах, а не наименьшими.

Перечисленные методы характеризуют метод поиска по симплексу как весьма полезный при проведении вычислений в реальном времени (анализ в динамике).

Недостатком метода является возможность возникновения трудностей, связанных с масштабированием, поскольку все координаты вершин симплекса зависят от одного и того же масштабного множителя альфа. Чтобы обойти трудности такого рода следует промасштабировать все переменные с тем, чтобы их значения были сравнимыми по величине.

4 Линейная оптимизация

Рассмотрим задачи, которые в математической литературе обычно называют линейным программированием, хотя термин «линейное программирование», появившийся до широкого использования ЭВМ, не соответствует современному пониманию смысла программирования.

Приведем краткую историческую справку.

В 1939 г. к Ленинградскому математику, позже академику, Л.Канторовичу обратились представители треста, выпускающего фанеру, с просьбой решить одну сугубо производственную задачу. Эта задача имела весьма локальный характер, а именно: как наилучшим образом распределить работу между станками? Дело в том что, такого рода производственные задачи имеют всегда целый ряд конкретных ограничений, с которыми вынужден считаться человек, взявшийся решать их.

Любое производство располагают ограниченными ресурсами. На заводе или цехе работает определенное количество людей, станков. Производительность станков также ограничена. Как и количество сырья, поступающего на переработку, как и многие другие ресурсы. В этих условиях требуется найти наилучший с позиций экономики способ ведения работ.

Решая такую локальную задачу, Канторович вывел определенные закономерности и создал новый метод, оказавшийся универсальным, который можно успешно применять, решая практически любую хозяйственную задачу.

Этот метод, созданный выдающимся советским ученым, получил название метода линейного программирования и широко используется в мировой практике. К нему прибегают, решая обширный класс хозяйственных задач, начиная с оптимизации грузопотоков и кончая разработкой перспективных планов для целых отраслей производства.

Новаторский научный поиск и открытие линейного программирования Л.В.Канторовичем отмечены Нобелевской премией по экономике за 1975 год.

Таким образом, линейное программирование возникло в связи с рассмотрением вопросов о нахождении наивыгоднейших вариантов при решении различных планово-производственных задач. В этих задачах имеется большая свобода изменения различных параметров и ряд ограничивающих условий. Требуется найти такие значения параметров, которые с некоторой точки зрения были бы наилучшими.

К таким задачам относятся задачи нахождения наиболее рационального способа использования ресурсов (сырья, материалов, финансов и т. д.), определения наивыгоднейших производственных режимов, оптимального распределения выпуска продукции по предприятиям, повышения эффективности работы транспорта (транспортная задача), составления рецептуры изготовления многокомпонентной смеси и т. п.

При автоматическом управлении производственным процессом эти задачи должны решаться автоматически и непрерывно. Поэтому знание методов решения подобных задач, необходимое для всякого инженера, для специалиста по информатике и автоматическому управлению становится особенно важным.

Date: 2015-05-23; view: 4303; Нарушение авторских прав