Метод градиента

В этом методе используется градиент функции . Градиентом функции в точке 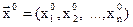называется вектор, проекциями которого на координатные оси являются частные производные функции по координатам (рис. 6.5)

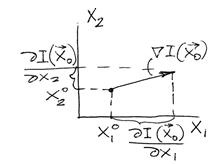
Рисунок 3.6 – Градиент функции

.

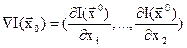Направление градиента – это направление наиболее быстрого возрастания функции (наиболее крутого “склона” поверхности отклика). Противоположное ему направление (направление антиградиента) – это направление наибыстрейшего убывания (направление наискорейшего “спуска” величин ).

Проекция градиента 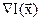на плоскость переменных перпендикулярна касательной к линии уровня 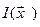, т.е. градиент ортогонален к линиям постоянного уровня целевой функции (рис. 3.6).

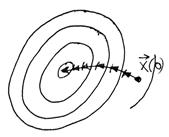
Рисунок 3.7 – Траектория движения к оптимуму в методе градиента

В отличие от метода релаксации в методе градиента шаги совершаются в направлении наибыстрейшего уменьшения (увеличения) функции .

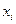Поиск оптимума производится в два этапа. На первом этапе находятся значения частных производных по всем переменным , которые определяют направление градиента в рассматриваемой точке. На втором этапе осуществляется шаг в направлении градиента при поиске максимума или в противоположном направлении – при поиске минимума.

Если аналитическое выражение неизвестно, то направление градиента определяется поиском на объекте пробных движений. Пусть 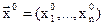начальная точка. Дается приращение 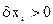величина 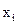, при этом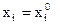 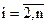. Определяют приращение 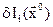и производную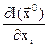

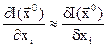
Аналогично определяют производные по остальным переменным. После нахождения составляющих градиента пробные движения прекращаются и начинаются рабочие шаги по выбранному направлению. Причем величина шага тем больше, чем больше абсолютная величина вектора .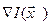

При выполнении шага одновременно изменяются значения всех независимых переменных. Каждая из них получает приращение, пропорциональное соответствующей составляющей градиента

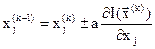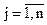, (3.10)

или в векторной форме

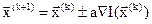, (3.11)

где 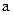– положительная константа; “+” – при поиске max I; “-” – при поиске min I.

Алгоритм градиентного поиска при нормировании градиента (деление на модуль) применяется в виде

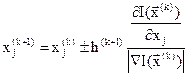; (3.12)

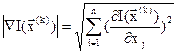(3.13)

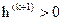определяет величину шага по направлению градиента.

Алгоритм (3.10) обладает тем достоинством, что при приближении к оптимуму длина шага 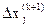автоматически уменьшается. А при алгоритме (3.12) стратегию изменения 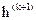можно строить независимо от абсолютной величины коэффициента.

В методе градиента каждый разделяется один рабочий шаг, после которого вновь вычисляются производные, определяется новое направление градиента и процесс поиска продолжается (рис. 3.5).

Если размер шага выбран слишком малым, то движение к оптимуму будет слишком долгим из-за необходимости вычисления в очень многих точках. Если же шаг выбран слишком большим, в район оптимума может возникнуть зацикливание.

Процесс поиска продолжается до тех пор, пока 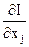, , 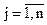не станут близки к нулю или пока не будет достигнута граница области задания переменных.

В алгоритме с автоматическим уточнением шага величину 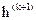уточняют так, чтобы изменение направления градиента 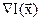в соседних точках 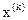и 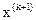улучшающей последовательности составляло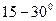 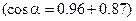(рис 3.7)

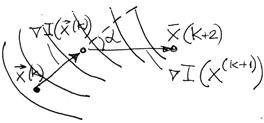
Рисунок 3.8 – Изменение направления градиента в соседних точках

Должно быть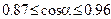

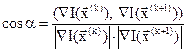
где 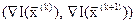– скалярное произведение векторов.

;

;

;

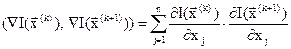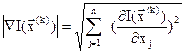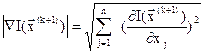Если ;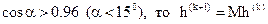

если ;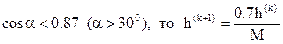

если ,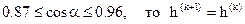

где .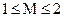

Критерии окончания поиска оптимума:

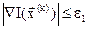; (3.14)

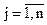, ; (3.15)

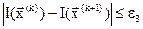; (3.16)

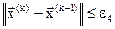; (3.17)

где 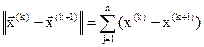– норма вектора.

Поиск завершается при выполнении одного из условий (3.14) – (3.17).

Недостатком градиентного поиска (так же и рассмотренных выше методов) является то, что при его использовании можно обнаружить только локальный экстремум функции . Для отыскания других локальных экстремумов необходимо производить поиск из других начальных точек.

Date: 2015-05-23; view: 806; Нарушение авторских прав