Метод сканирования

Идея алгоритма перебора крайне проста. Вычисляют значения функции в конечном числе точек 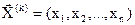области D_x (в узлах координатной сетки).Из вычисленных значений выбирают наименьшее (наибольшее) 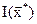. Координаты соответствующего узла сетки 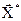– это координаты экстремума, определённые с точностью до , где – h шаг сетки (рис. 6.10).

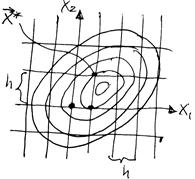
Рисунок 3.11 – Поиск оптимума на сетке переменных

Точность определения точки минимума, причем глобального, зависит от плотности наполнения области D_x дискретным множеством 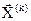, то есть от величины шага h координатной сетки, тем выше точность определения положения оптимума, однако при уменьшении h быстро растёт объём вычислений. Если интервал изменения каждой переменной разбить К равных частей, то h равно

,

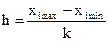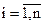
При этом необходимое количество вычислений I(x) равно

.

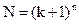Поэтому эффективное применение данного метода ограничивается задачами невысокой размерности (n=2-3). При большой размерности вектора 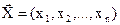требуется выполнение большого объёма вычислительной работы.

Пусть область D_x – геперкуб:

,

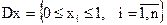в котором ищется 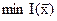.Точность определения координат вектора 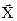, минимизирующего , положим равной 0,1. Тогда интервалы 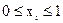следует разбить на 10 частей с шагом h=0,1 плоскостями, ортогональными 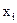и вычислить во всех точках перечисления плоскостей значения . Всего потребуется вычислить в 11ⁿ точках. Пусть для нахождения I в каждой точке требуется примерно 10²n арифметических операций. Тогда общее число арифметических операций алгоритма перебора примерно 11⁽ⁿ⁺²⁾n и при n=10 на ЭВМ с быстродействием 10⁹ oп/c требуется примерно 10⁴ с, т.е. примерно 167 минут непрерывной работы ЭВМ.

Иногда поиск осуществляется с переменным шагом сканирования. Вначале величина h выбирается достаточно большой, выполняется грубый поиск для локализации экстремума, а поиск в районе оптимума осуществляется с меньшим шагом.

Достоинства метода – возможность определения глобального оптимума и независимость поиска от вида оптимизируемой функции.

3.3.2 Метод Гаусса-Зейделя

Метод Гаусса-Зейделя, называемый также методом покоординатного спуска, аналогичен методу релаксации. Отличие заключается лишь в том что, в этом методе не определяется осевое направление, вдоль которого значение 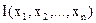изменяется наиболее сильно. Поочерёдно изменяются все переменные.

Алгоритм поиска минимума следующий. Пусть ищется минимум . Устанавливается очерёдность изменения 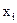– 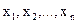и начальная точка поиска. Затем все переменные 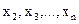фиксируются на уровне 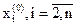, 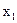изменяется по алгоритму

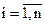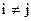; ; ; (3.22)

где 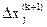– шаг изменяется 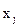, обычно 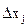не зависит от k.

После каждого шага вычисляется , сравнивается с предыдущим значением, критерия шаги продолжаются до достижения частного оптимума по x_j = x₁. В этой точке величина 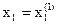фиксируется и изменяется x₂ до достижения оптимума по x₂ и т.д. После того как достигается оптимум по последней переменной x_n, снова изменяется x₁ и весь цикл повторяется до тех пор, пока не будет найдена точка оптимума.

На рисунке 3.11 показан алгоритм поиска минимума для функции двух переменных.

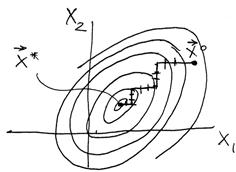
Рисунок 3.12 – Траектория движения к оптимуму в методе координатного спуска

Заметим что для функции двух переменных методы релаксации и Гаусса-Зейделя совпадают.

Если первый шаг изменения x_j не улучшает значение критерия, т.е.

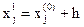, а 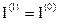, то выполняется шаг по x_j в обратном направлении

,

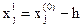т. е. Первый шаг пробный. Если и этот шаг неудачный, то переходят к изменению x_j+1 и т.д.

Поиск заканчивают когда достигается точка 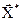, из которой при движении в любом осевом направлении улучшение критерия не наблюдается.

Рассмотрим вопрос улучшения алгоритма поиска .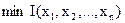

Пусть в области допустимых решений D задано нулевое приближение .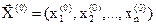

Рассматриваем функцию при фиксированных значениях 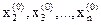как функцию одной переменной x₁, т. е.

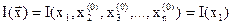. (3.23)

Минимизируя 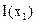находим значение 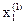, доставляющее минимум функцию (3.23):

;

.

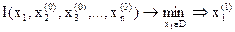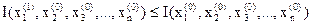Далее при фиксированных значениях 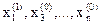рассматриваем 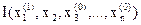как функцию одной переменной x₂. Находим её минимум

;

.

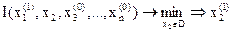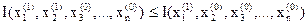Продолжая эту процедуру последовательно, после n шагов получаем точку 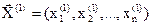, в которой выполняется условие

.

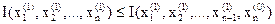В результате одного шага покоординатного спуска происходит переход из начальной точки 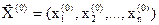в точку 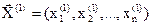. Если при этом оказывается, что

,

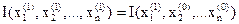то начальная точка 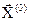– точка, доставляющая минимум функцию .

Если 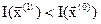,то выполняется следующий шаг покоординатного спуска, в котором за начальную точку принимается 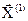,получаем 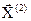и т.д. Этот процесс продолжается до тех пор пока не выполнится какое-либо условие окончания поиска, например такое

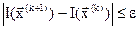, (3.24)

где – заданная точность.

или

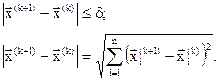(3.25)

Таким образом, поиск минимума функции одной переменной занимает центральное место в рассматриваемом алгоритме покоординатного спуска.

Простота метода и сравнительно небольшой объём вычислений обусловили его распространение в автоматических системах поиска.

Date: 2015-05-23; view: 1588; Нарушение авторских прав