
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Парабола и её каноническое уравнение
|
|
Определение. Параболой называется геометрическое место точек, для каждой из которых расстояние до некоторой фиксированной точки плоскости, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, не проходящей через фокус и называемой директрисой.
Определение. Расстояние от фокуса параболы до её директрисы называется параметром параболы. Эксцентриситет параболы принимается равным единице.
Опустим из фокуса 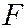 перпендикуляр на директрису
перпендикуляр на директрису 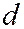 и точку пересечения этого перпендикуляра с директрисой параболы обозначим буквой
и точку пересечения этого перпендикуляра с директрисой параболы обозначим буквой 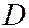 . Введём на плоскости ДПСК, поместив начало координат
. Введём на плоскости ДПСК, поместив начало координат 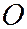 в центре отрезка
в центре отрезка 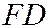 , принимая за ось
, принимая за ось 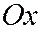 прямую
прямую 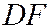 , с положительным направлением от
, с положительным направлением от 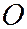 к
к  (См. рис.176).
(См. рис.176).
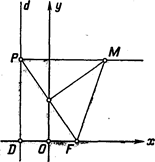
Рис. 176
|
Расстояние 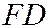 от фокуса
от фокуса  до директрисы
до директрисы 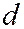 обозначим буквой
обозначим буквой 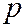 (это параметр параболы). В выбранной системе координат фокус
(это параметр параболы). В выбранной системе координат фокус 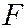 имеет координаты
имеет координаты 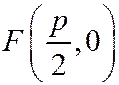 . Уравнение директрисы
. Уравнение директрисы 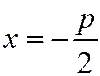 .
.
Пусть 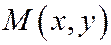 - произвольная точка плоскости. Обозначим через
- произвольная точка плоскости. Обозначим через 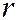 расстояние
расстояние 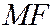 от точки
от точки 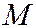 до фокуса
до фокуса 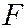 параболы, а через
параболы, а через 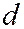 - расстояние
- расстояние 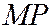 от точки
от точки 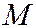 до директрисы этой параболы.
до директрисы этой параболы.
Точка 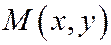 лежит на данной параболе тогда и
лежит на данной параболе тогда и
только тогда, когда  . Так как
. Так как 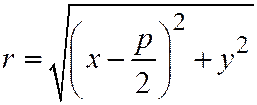 ,
,
а 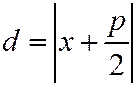 , то уравнение параболы имеет вид:
, то уравнение параболы имеет вид:
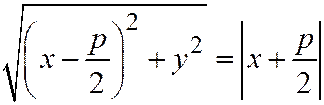 . Это уравнение эквивалентно следующему уравнению:
. Это уравнение эквивалентно следующему уравнению: 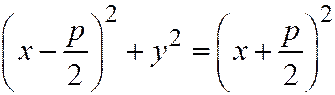 .
.
Или: 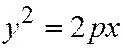 (1)
(1)
Определение. Уравнение (1) называется каноническим уравнением параболы.
§ 121. Исследование формы параболы.
Так как ордината 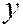 в каноническое уравнение параболы входит во второй степени, то ось
в каноническое уравнение параболы входит во второй степени, то ось 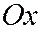 является осью симметрии параболы
является осью симметрии параболы 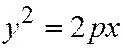 .
.
Определение. Точка пересечения параболы с её осью симметрии называется вершиной параболы. Парабола (1) имеет только одну вершину 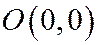 .
.
Из уравнения 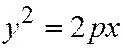 следует, что
следует, что 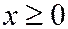 (т.к.
(т.к. 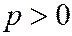 , а
, а 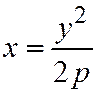 ). Разрешая уравнение
). Разрешая уравнение 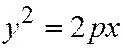 относительно
относительно 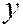 и беря для
и беря для 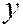 лишь неотрицательное значение
лишь неотрицательное значение 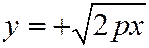 , видим, что в полуинтервале
, видим, что в полуинтервале 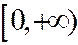
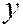 - возрастающая функция
- возрастающая функция 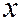 , причём
, причём 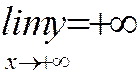 .
.
Всякая прямая пересекает параболу не более чем в двух точках (т.к. прямая определяется уравнением первой степени, а парабола - второй. Проведённое исследование даёт представление о форме параболы (См. рис. 177).
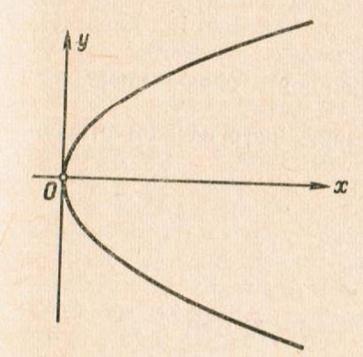
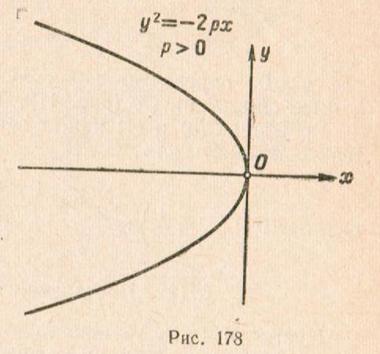
Рис. 177
Замечание. Уравнение 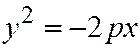 , где
, где 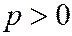 сводится к уравнению
сводится к уравнению 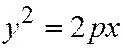 заменой
заменой 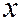 на
на 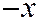 , т.е. путём преобразования системы координат, которое соответствует изменению положительного направления оси
, т.е. путём преобразования системы координат, которое соответствует изменению положительного направления оси 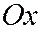 на противоположное.
на противоположное.
Отсюда следует, что парабола 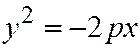 симметрична с параболой
симметрична с параболой 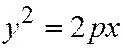 относительно оси
относительно оси 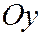 (См. рис.178). Аналогичными рассуждениями устанавливаем, чтокаждое из уравнений:
(См. рис.178). Аналогичными рассуждениями устанавливаем, чтокаждое из уравнений: 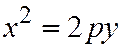 ;
; 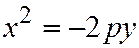 (2) где
(2) где 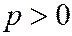 определяет параболу с вершиной в начале координат и осью симметрии
определяет параболу с вершиной в начале координат и осью симметрии 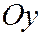 (См. рис. 179, 180).
(См. рис. 179, 180).
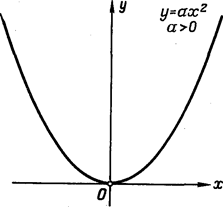
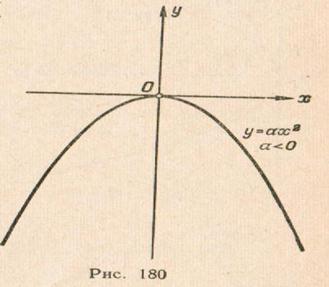
Рис. 179
Уравнение (2) пишут часто в виде, разрешённом относительно ординаты 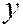 :
: 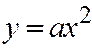 , где
, где 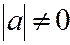 ; (
; (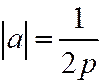 ).
).
§ 123. Касательная к параболе.
В курсе математического анализа доказывается, что если функция 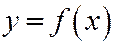 в точке
в точке 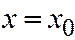 имеет производную, то уравнение касательной к линии, выражаемой уравнением
имеет производную, то уравнение касательной к линии, выражаемой уравнением 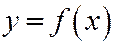 в точке
в точке 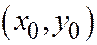 , где
, где 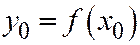 имеет вид:
имеет вид: 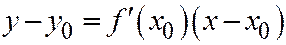 . Теперь, если парабола задана уравнением
. Теперь, если парабола задана уравнением 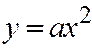 ,
, 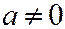 , то уравнение касательной к ней в точке
, то уравнение касательной к ней в точке 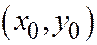 будет иметь вид:
будет иметь вид: 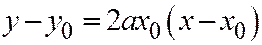 . Раскрываем скобки:
. Раскрываем скобки: 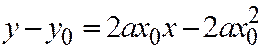 , и, т.к.
, и, т.к.  , откуда
, откуда 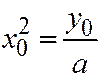 , то
, то 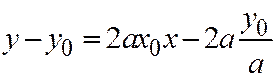 или
или 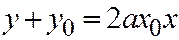 (3)
(3)
Полагая в уравнении (3) 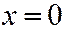 , находим точку
, находим точку 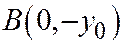 , пересечения касательной к параболе (3) с её осью симметрии.
, пересечения касательной к параболе (3) с её осью симметрии.
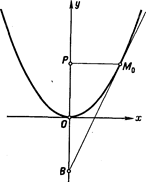
Отсюда вытекает следующий способ построения касательной к параболе в данной точке 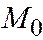 . Опускаем из точки
. Опускаем из точки 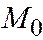 перпендикуляр
перпендикуляр 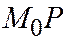 на ось симметрии параболы и откладываем на оси симметрии параболы отрезок
на ось симметрии параболы и откладываем на оси симметрии параболы отрезок 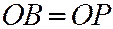 (См. рис.). Прямая
(См. рис.). Прямая 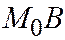 и будет касательной к параболе в точке
и будет касательной к параболе в точке 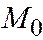 .
.
§ 124. Оптическое свойство параболы.
 Теорема 1. Касательная к параболе является биссектрисой угла
Теорема 1. Касательная к параболе является биссектрисой угла 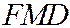 между фокальным радиусом
между фокальным радиусом 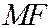 точки касания и перпендикуляром
точки касания и перпендикуляром 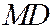 , опущенным из точки касания на директрису.
, опущенным из точки касания на директрису.
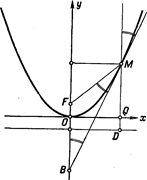
Рис. 183. Рис. 184.
Доказательство. Имеем (См. рис. 184): 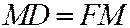 ,
, 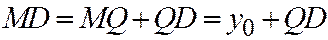 . Но
. Но 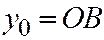 ,
, 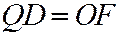 . Следо-вательно:
. Следо-вательно: 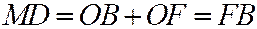 , т.е.
, т.е.  . Поэтому треугольник
. Поэтому треугольник 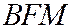 равнобедренный и, значит:
равнобедренный и, значит: 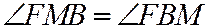 ; но
; но 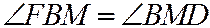 ; следовательно
; следовательно 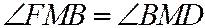 . Что и требовалось доказать.
. Что и требовалось доказать.
Эта теорема имеет следующее оптическое истолкование: если в фокусе 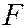 параболического зеркала поместить источник света, то лучи, отразившись от зеркала, образуют пучок параллельных лучей. Указанное свойство параболического зеркала применяется при устройстве зеркальных прожекторов.
параболического зеркала поместить источник света, то лучи, отразившись от зеркала, образуют пучок параллельных лучей. Указанное свойство параболического зеркала применяется при устройстве зеркальных прожекторов.
§ 125. Полярное уравнение эллипса, гиперболы и параболы.
Часто используют уравнения эллипса, гиперболы и параболы в полярной системе координат. Мы фиксируем полюс полярной системы координат в фокусе кривой. При этом для эллипса выбираем левый фокус, а для гиперболы - правый. Полярную ось выбираем так, чтобы её направление совпадало с положительным направлением оси абсцисс.
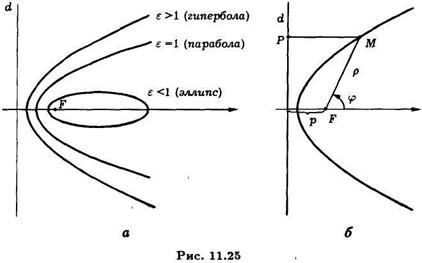
Все три вида кривых описываются общим свойством: для любой точки отношение расстояний до фокуса и до директрисы постоянно и равно эксцентриситету кривой. Значение эксцентриситета определяет тип кривой. Если зафиксировать фокальный параметр (это расстояние от фокуса до директрисы) так, что положение директрисы в выбранной системе координат будет оставаться неизменным, то варьируя эксцентриситет, получим единый ряд эллипсов, параболы, правых ветвей гипербол (См. рис. 11.25). Конкретная кривая определяется своим эксцентриситетом 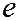 при помощи уравнения:
при помощи уравнения: 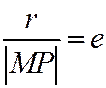 , (4)
, (4)
где 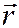 - полярный, он же фокальный радиус точки
- полярный, он же фокальный радиус точки 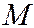 на кривой,
на кривой,  - перпендикуляр, опущенный из точки
- перпендикуляр, опущенный из точки 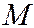 на директрису
на директрису 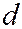 (См. рис. 11.25).
(См. рис. 11.25).
|
Так как 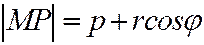 , то подставив это выражение в (4), получим:
, то подставив это выражение в (4), получим: 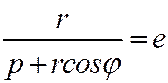 или
или 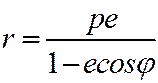 (5)
(5)
Уравнение (5) называется полярным уравнением эллипса, параболы, правой ветви гиперболы.
§ 126. Эллипс, гипербола и парабола как конические сечения.
Рассмотрим поверхность прямого кругового конуса, неограниченно простирающегося по обе стороны от его вершины.
Плоскость, проходящая через вершину конуса может занимать относительно этого конуса следующие три положения:
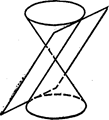
1) Иметь с конусом только одну общую точку (вершину конуса (См. рис.187)).
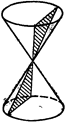
2) Касаться конуса вдоль его образующей (См. рис.188).
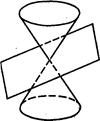
3) Пересекать конус по двум различным его образующим (См. рис.189).
|
|
|
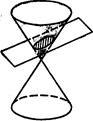
Плоскость, не проходящая через вершину конуса, может занимать относительно конуса также три различных положения: 1) Пересекать все образующие конуса (См.рис.190)
|
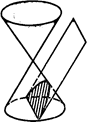
2) Быть параллельной только одной образующей конуса (См. рис.191).
|
3) Быть параллельной двум различным образующим конуса (См. рис.192).
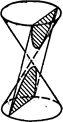
|
Теорема 2. Плоскость, не проходящая через вершину прямого кругового конуса, пересекает его по эллипсу, если она пересекает все образующие конуса (См. рис.190), по параболе, если она параллельна только одной образующей конуса (См. рис.191) и по гиперболе, если она параллельна двум образующим конуса (См. рис.192).
Доказательство. Для доказательства рассмотрим прямой круговой конус, который в прямоугольной системе координат 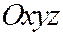 описывается уравнением:
описывается уравнением:
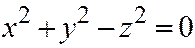 (6)
(6)
и геометрически получается при вращении вокруг оси 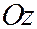 прямой
прямой 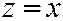 , принадлежащей координатной плос-кости
, принадлежащей координатной плос-кости 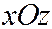 . В силу круговой симметрии поверхности (6) можно ограничиться только сечениями при помо-щи плоскостей, перпендикулярных координатной пло-скости
. В силу круговой симметрии поверхности (6) можно ограничиться только сечениями при помо-щи плоскостей, перпендикулярных координатной пло-скости 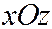 . Таким плоскостям соответствуют уравнения
. Таким плоскостям соответствуют уравнения 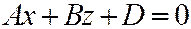 ,
, 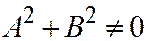 .
.
Если 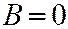 , то секущая плоскость описывается уравнением
, то секущая плоскость описывается уравнением 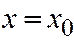 , где
, где 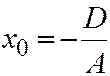 и параллельна координатной плоскости
и параллельна координатной плоскости 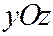 . Подставив значение абсциссы
. Подставив значение абсциссы 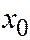 в уравнение конуса (6), найдём, что сечение в плоскости
в уравнение конуса (6), найдём, что сечение в плоскости 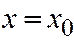 описывается уравнением
описывается уравнением 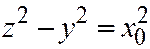 и при
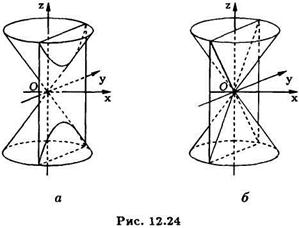
и при 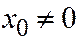 определяет собой равностороннюю гиперболу (См. рис.12.24), а при
определяет собой равностороннюю гиперболу (См. рис.12.24), а при 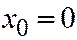 пару прямых, которые являются образующими конусам. Рис.12.24.
пару прямых, которые являются образующими конусам. Рис.12.24.
Пусть теперь в уравнении секущей плоскости коэффициент 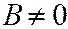 . Тогда плоскость можно представить уравнением
. Тогда плоскость можно представить уравнением 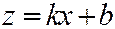 , где
, где 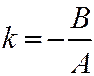 ,
, 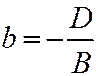 . В силу симметрии конуса относительно плоскости
. В силу симметрии конуса относительно плоскости 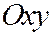 достаточно ограничиться случаем, когда
достаточно ограничиться случаем, когда 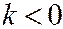 .
.
Коническое сечение для рассматриваемой плоскости в пространстве будет описываться системой двух уравнений 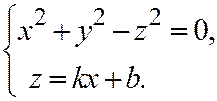 (7)
(7)
Чтобы получить уравнение секущей плоскости, рассмотрим прямоугольную систему координат 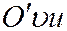 ,
,
|
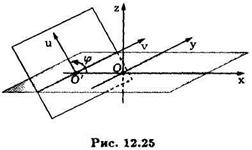
взяв в качестве координатных осей 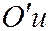 и
и 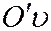 прямые, являющиеся пересечением секущей плоскости с координатными плоскостями
прямые, являющиеся пересечением секущей плоскости с координатными плоскостями 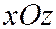 и
и 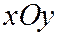 (См.рис. 12.25).
(См.рис. 12.25).
Координаты 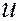 и
и 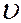 произвольной точки в секущей плоскости будут связаны с её координатами
произвольной точки в секущей плоскости будут связаны с её координатами 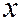 ,
, 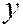 и
и 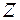 в пространстве соотношениями:
в пространстве соотношениями:
 (8)
(8)
где 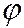 - угол между коническим сечением, перпендикулярным координатной плоскости
- угол между коническим сечением, перпендикулярным координатной плоскости 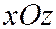 , и координатной плоскостью
, и координатной плоскостью 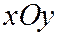 , причём
, причём 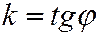 , а
, а 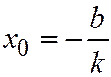 .
.
Подставляя (8) в первое уравнение системы (7), т.е. в уравнение 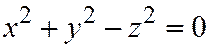 , получим уравнение конического сечения в системе координат
, получим уравнение конического сечения в системе координат 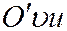 :
:
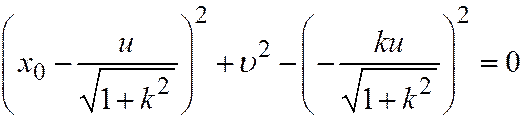 . Раскрывая скобки и приводя подобные члены, находим:
. Раскрывая скобки и приводя подобные члены, находим:
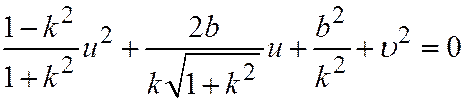 . (9)
. (9)
При 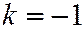 , когда секущая плоскость образует с плоскостью
, когда секущая плоскость образует с плоскостью 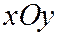 тот же угол, что и образующие конуса, конические сечения будут представлять собой параболы (См. рис.) и описываться уравнением:
тот же угол, что и образующие конуса, конические сечения будут представлять собой параболы (См. рис.) и описываться уравнением:
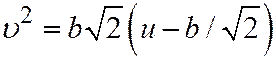 .
.
Варьируя параметр 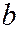 в уравнении секущей плоскости, в качестве конического сечения можно получить любую параболу.
в уравнении секущей плоскости, в качестве конического сечения можно получить любую параболу.
При 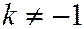 ,
, 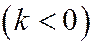 уравнение (9) принимает вид:
уравнение (9) принимает вид:
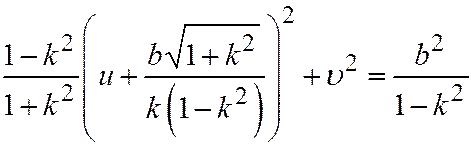 . (10)
. (10)
Здесь возможны два варианта. При 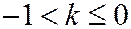 , т.е. когда секущая образует с плоскостью
, т.е. когда секущая образует с плоскостью 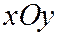 меньший угол, чем образующие конуса, будет выполнено неравенство
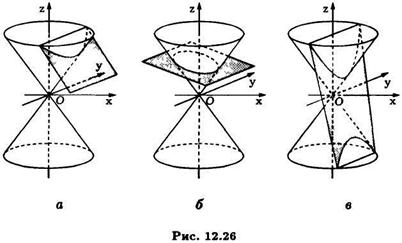
меньший угол, чем образующие конуса, будет выполнено неравенство 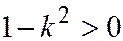 и поэтому уравнение (10) конического сечения будет уравнением эллипса (См. рис. 12.26).
и поэтому уравнение (10) конического сечения будет уравнением эллипса (См. рис. 12.26).
|
И здесь варьируя параметры 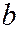 и
и 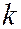 в уравнении секущей плоскости, мы можем получить в сечении любой эллипс.
в уравнении секущей плоскости, мы можем получить в сечении любой эллипс.
При 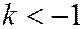 , т.е. когда секущая плоскость образует с плоскостью
, т.е. когда секущая плоскость образует с плоскостью 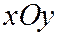 больший угол, чем образующие конуса, имеем
больший угол, чем образующие конуса, имеем 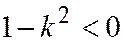 , так что коническое сечение, описываемое уравнением (10) будет являться гиперболой (См. рис.). Варьируя параметры
, так что коническое сечение, описываемое уравнением (10) будет являться гиперболой (См. рис.). Варьируя параметры 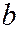 и
и 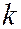 можно получить в коническом сечении любую гиперболу.
можно получить в коническом сечении любую гиперболу.
Date: 2015-05-22; view: 991; Нарушение авторских прав