Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Примеры. Построить прямую, заданную уравнениями
|
|
Построить прямую, заданную уравнениями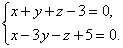 
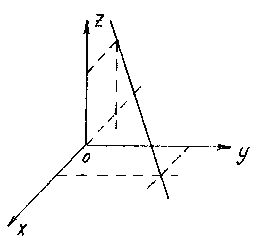Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:
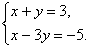
Решив эту систему, найдем точку M 1(1;2;0).
Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz:
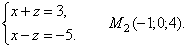
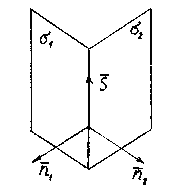От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор 
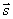прямой.
Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам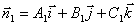 
и 
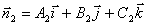. Поэтому за направляющий вектор 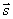прямой l можно взять векторное произведение нормальных векторов:
.
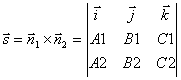Пример. Привести общие уравнения прямой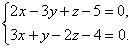 
к каноническому виду.
Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:
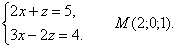
Нормальные векторы плоскостей, определяющих прямую имеют координаты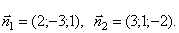 
Поэтому направляющий вектор прямой будет
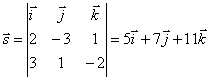. Следовательно, l: 
.
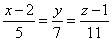Date: 2015-05-22; view: 834; Нарушение авторских прав