Отношения между множествами

Наглядно отношения между множествами изображают при помощи особых чертежей, называемых КРУГАМИ ЭЙЛЕРА (или диаграммами Эйлера – Венна).

Для этого множества, сколько бы они ни содержали элементов, представляют в виде кругов или любых других замкнутых кривых (фигур) – рис.1.

Рис. 1.

1. Пусть даны два множества: X={a; b; c; d} иY={l; k; m; b; c}. Множества Х и Y содержат некоторые одинаковые элементы, а именно “b” и “c”. В данном случае говорят, что множества X иY находятся в отношении ПЕРЕСЕЧЕНИЯ. С помощью кругов Эйлера данное отношение можно представить в виде рис. 2.

X Y B₁ B₂

Рис. 2. Рис. 3.

2. Пусть даны множества B₁={1; 2; 3} и B₂={4; 5; 6}.

Данные множества различны, у них нет одинаковых элементов. В таком случае говорят, что множества B₁ и B₂ находятся в отношении НЕПЕРЕСЕЧЕНИЯ.

С помощью кругов Эйлера данное отношение показано на рис. 3.

3. Пусть даны множества A={a; b; c; d; e} и B={a; b; c}.

Очевидно, что эти множества пересекаются; кроме того, каждый элемент
множества В является в то же время (одновременно) и элементом множества А. Тогда говорят, что множество В ВКЛЮЧЕНО в множество А, или что В есть ПОДМНОЖЕСТВО множества А.

Определение 1.1

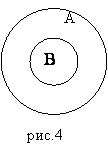Множество В является подмножеством множества А тогда и только тогда, когда каждый элемент множества В является элементом множества А.

Отношение “включено” обозначается знаком Ì.

Соответственно отношение “включает” – знаком É.

Определение 1.1 символически записывается так: ВÌА или АÉВ. С помощью кругов Эйлера данное отношение между множествами показано на рис.4.

Из определения подмножества следует, что всякое непустое множество А содержит по крайней мере два

множества: Ø и А, которые называются НЕСОБСТВЕННЫМИ

ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. Все остальные подмножества (если они существуют) называются СОБСТВЕННЫМИ ПОДМНОЖЕСТВАМИ МНОЖЕСТВА. То есть, если В – собственное подмножество множества А, то имеем: ØÌ ВÌА, или иначе: АÉВÉ Ø.

4. Пусть даны множества C={x; y; z}, D={x; y; z}, которые состоят из одних и тех же элементов. В таком случае говорят, что множества С иD равны и пишут C=D.

Определение 1.2

Множества С и D называются равными, если они состоят из одних и тех же элементов.

Используя понятие “включено”, можно дать другое определение равенства множеств.

Определение 1.3

Множества C и D называются равными тогда и только тогда, когда множество С является подмножеством множества D, и наоборот.

Символически данное определение можно записать так:
С = D Û С Ì D и D Ì С, или С = D Û С Ì D Ù D Ì С,
где знак Û означает “эквивалентность” (равнозначность), а знак Ù (конъюнкция) означает одновременность (совместность) осуществления тех операций (или событий), которые он соединяет.

С помощью кругов Эйлера отношение “равенство” показано на рис.5.

Рис.5. рис.6.

Универсальное множество.

Пусть U (или T – total) – некоторое фиксированное множество. Рассмотрим только такие множества А, В, С,…, которые являются подмножествами множества U. В этом случае множество U называется универсальным множеством всех множеств А, В, С,…

Примером универсального множества может служить множество действительных чисел, множество людей на планете Земля…

Мы его будем изображать прямоугольником с буквой U в правом верхнем углу (рис.6), внутри которого будут размещаться те или иные множества.

Date: 2015-04-23; view: 949; Нарушение авторских прав