Функциональное уравнение Беллмана

В основе метода по оптимизации любого оборудования путем принятия решения по замене его новым, лежит принцип оптимальности Беллмана: на каждом этапе принимается такое решение, которое обеспечивает оптимальность с данного этапа до конца процесса, то есть на каждом этапе необходимо принимать решение, просматривая его последствия до самого конца процесса. Если считать все этапы независимыми друг от друга, то оптимальным будет то решение, которое приносит максимальный выигрыш именно на данном этапе. Но, например, при покупке новой техники в замен устаревшей на ее приобретение затрачиваются определенные средства. Поэтому прибыль от ее эксплуатации вначале может быть небольшой. Однако в следующие годы новая техника будет приносить большую прибыль. И наоборот, если руководитель примет решение оставить старую технику для получения прибыли в текущем году, то в дальнейшем это приведет к значительным убыткам. Данный пример демонстрирует следующий факт: в многошаговых процессах все шаги зависят друг от друга, и, следовательно, управление на каждом конкретном шаге надо выбирать с учетом его будущих воздействий на этот процесс.

Известна стоимость нового оборудования С денежных единиц. Эксплуатация оборудования возраста t лет в течении I года приносит прибыль U(t) денежных единиц. Требуется определить оптимальную политику замены оборудования таким образом, чтобы прибыль, полученная при эксплуатации нового оборудования в течение n лет, была максимальной.

Предположим, что решение – заменить или оставить оборудование принимаем в начале года.

Введем функцию Беллмана f_k(t) – максимальная прибыль, которая может быть получена при эксплуатации автомобиля возраста t в течении k лет (при оптимальной политике замены).

Составим первое уравнение Беллмана.

Пусть f₁(t) – максимальная прибыль, которая может быть получена при эксплуатации автомобиля возраста t в течение I года.

Если в начале года примем решение сохранить оборудование, то прибыль будет равна U(t). Если в начале года примем решение заменить автомобиль, то должны потратить на покупку нового автомобиля С рублей, а прибыль, которая принесет эксплуатация нового автомобиля в течении года, равнаU(С).

Таким образом, прибыль, полученная в случае замены автомобиля в течение года, равна: - C + U(0).

Отсюда:

f₁(t) = max (U(t); - C + U(0)). (2.20)

Выведем функциональное уравнение Беллмана для функции f_k+1(t).

Предположим, что в начале первого года эксплуатации автомобиля было принято решение сохранить его, тогда прибыль за I год эксплуатации составит U(t).

По истечении года возраст оборудования будет равен t + I год, а срок оставшейся эксплуатации автомобиля равен k лет.

В соответствии с принципом оптимальности, необходимо постараться получить за оставшиеся k лет максимальных доход, т.е. f_k(t + 1).

Итак, если в начале срока эксплуатации сохранить автомобиль, то прибыль за k + 1 год составит сумму:

U(t) + f_k(t + 1). (2.21)

Предположим, в начале рассматриваемого срока принято решение заменить автомобиль, тогда, потратив С рублей на покупку нового автомобиля, получим за год эксплуатации прибыль U(0). Через год возраст автомобиля будет равен I году, срок оставшейся эксплуатации k лет и максимальная прибыль, которую можно получить за оставшиеся k лет, составит f_k(1). Значит, за k + 1 год в случае «замены» прибыль будет равна:

-С + U(0) + f_k(1). (2.22)

Для определения функции f_{k +1}(t) необходимо выбрать наибольшее из чисел: U(t) + f_k(t + 1); - C + U(0) + f_k(1), т.е.

f_k+1(t) = max (U(t) + f_k(t + 1); -C + U(0) + f_k(1)). (2.23)

Это и есть функциональное уравнение Беллмана.

Выводы

Все закономерности, существующие в природе и технике делятся на функциональные (детерминированные) и случайные (вероятностные, стохастические).

Для функциональных закономерностей характерна жесткая связь между функцией отклика и аргументом, то есть определенному значению аргумента соответствует определенное значение функции. Случайные закономерности существуют тогда, когда зависимая переменная определяется не только независимой переменной, но и рядом случайных факторов.

Для решения задач дипломного проекта берется 1 тип закономерности класса 1а (закономерности изменения качества автомобилей по наработке). Из книги Н.С. Захарова «Моделирование процессов изменения качества автомобилей» /5, ст.50/ для моделирования закономерностей класса 1а используются аналитические функции следующего вида:

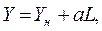(2.24)

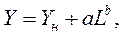(2.25)

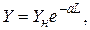(2.26)

где Y_н - начальное значение показателя качества;

a, b - параметры математической модели, характеризующие скорость изменения Y при увеличении L.

И так вид математической модели закономерности изменения интенсивности эксплуатации автомобиля от срока службы:

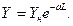(2.27)

Такой же вид имеет математическая модель изменения затрат на эксплуатацию автомобиля от срока службы.

Для определения оптимального срока эксплуатации вводится метод функционального уравнения Беллмана.