Кручение стержня эллиптического сечения

В качестве примера рассмотрим стержень эллиптического сечения (рис. 3.35).

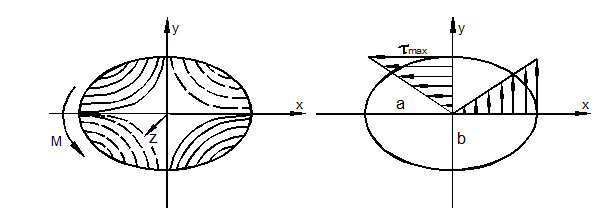
а) б)

Рис. 3.35

Уравнение контура эллипса:

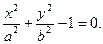
Для функции напряжений примем выражение

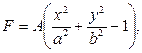(123)

которое удовлетворяет граничному условию F = 0, на контуре сечения.

Подставляя выражение (123) в уравнение Пуассона (120), получим:

Крутящий момент, согласно (122), равен:

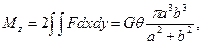
откуда

.

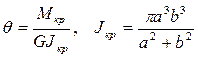Напряжения (119):

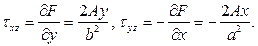
Полное напряжение (117):

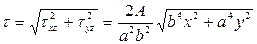
или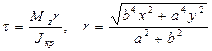

Распределение напряжений показано на рис. 3.35, б. Максимальное напряжение имеет место на концах малой оси эллипса.

Кручение стержня прямоугольного сечения

Рассмотрим сначала стержень узкого прямоугольного поперечного сечения (рис. 3.36, а).

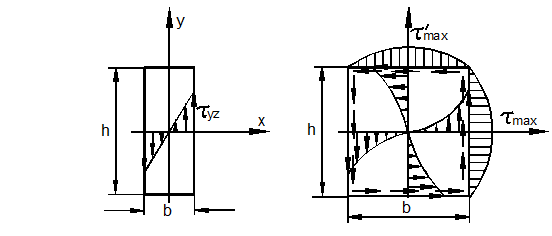
а) б)

Рис. 3.36

В этом случае будем пренебрегать выполнением граничных условий на коротких сторонах при 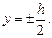Примем функцию напряжений в виде

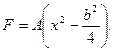(124)

В таком виде граничное условие F = 0 на длинных сторонах при 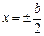будет удовлетворено.

Подставляя предполагаемое решение в уравнение (120) Пуассона, получим 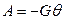. Напряжения (119):

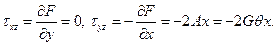
Полное напряжение (117):

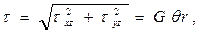(125)

где .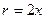

Крутящий момент 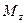(122):

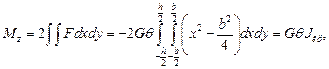(126)

где

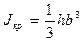(127)

Из (125), (126) следует:

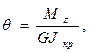
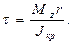(128)

Максимальное напряжение имеет место в середине длинной стороны сечения, где :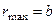

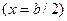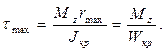(129)

где

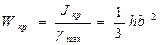(130)

- момент сопротивления узкого прямоугольного сечения.

Пусть теперь отношение сторон h/b одного порядка. Решение уравнения Пуассона представим в виде:

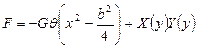, (131)

где первое слагаемое представляет его частное решение, а второе – решение однородного уравнения Лапласа 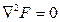в форме Фурье. На контуре сечения F = 0. Поэтому граничные условия можно записать в виде:

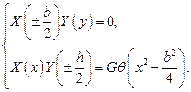(132)

Подставляя (131) в уравнение Пуассона (120), получим:

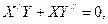
откуда, разделяя переменные:

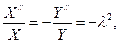
или

.

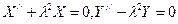Решения этих уравнений имеют вид:

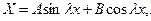
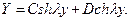
Удовлетворяя полученное решение граничным условиям (132) и учитывая симметрию функций 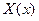, 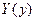относительно осей х, у, получим, что А = 0, С = 0, 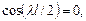откуда следует 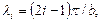где i = 1,2,3,….

В результате функция F принимает вид

.

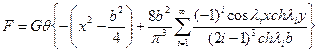Далее, согласно (122), вычисляем:

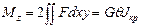
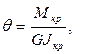(133)

где

(134)

Напряжения (119):

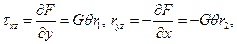(135)

где

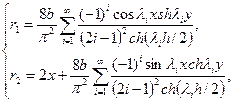(136)

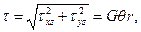
или

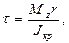(137)

а величины 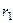, 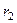определяются согласно (136).

Наибольшее значение 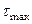имеет место при h > b в середине длинной стороны при 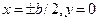. В этом случае , , ,

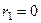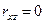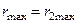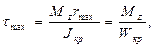(138)

где

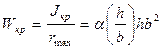(139)

- геометрический момент сопротивления кручению,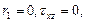

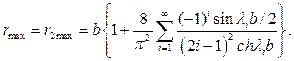(140)

Для практических расчётов достаточно взять i = 1, т.е. сохранив в рядах одно слагаемое.

Для вычисления 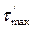в середине короткой стороны следует принять в (136) 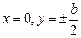. В результате получим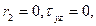

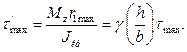(141)

Значения коэффициентов 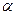, , 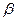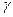в зависимости от отношения сторон 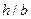приведены в справочных данных.

Таким образом, мы показали, что задача о кручении стержня прямоугольного сечения может быть решена строгими методами теории упругости.

Date: 2015-05-22; view: 828; Нарушение авторских прав