Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Кручение призматических стержней произвольного поперечного сечения
|
|
Рассмотрим стержень произвольного сплошного поперечного сечения, который закреплён на одном конце и скручивается моментом М на другом (рис. 3.33).
Рис. 3.33
Вводим гипотезу жёсткого контура, согласно которой контур сечения поворачивается как жёсткое целое, а площадь сечения может исказиться.
Под действием момента правое свободное торцевое сечение повернётся относительно левого на угол:
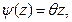(108)
где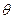 
- угол закручивания на единицу длины. Перемещения u и v произвольной точки А в плоскости сечения:
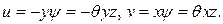(109)
Так как гипотеза плоских сечений в общем случае произвольного сечения на выносливость, осевое перемещение
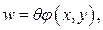(110)
где функция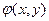 
называется функцией кручения Сен-Венана. Она характеризует искажение (депланацию) поперечного сечения.
Согласно (109), (110) и соотношениям Коши (83) получаем:
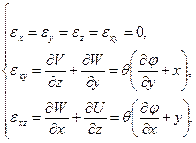
В соответствии с обобщённым законом Гука (21) находим:
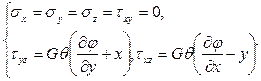(111)
Считая в уравнениях равновесия Коши (100) объёмные силы равными нулю и подставляя в них выражения (111), получим, что первые два уравнения тождественно удовлетворятся, а третье примет вид:
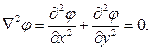(112)
Полученное уравнение в частных производных (112) называется гармоническим уравнением Лапласа.
На боковой поверхности стержня внешние силы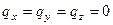 
, 
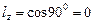и граничные условия (102) принимают вид
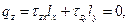
или
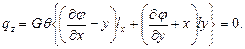(113)
Крутящий момент в поперечном сечении
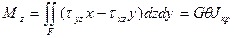(114)
где
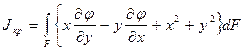(115)
- геометрическая жёсткость стержня при кручении.
Из (114) следует:
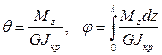(116)
Полное касательное напряжение:
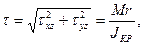(117)
где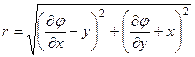 
(118)
Из (117), (118) видно, что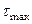 
возникает при 
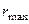в опасной точке сечения, которая не обязательно наиболее удалённая.
Таким образом, задача о кручении призматического стержня сводится к решению гармонического уравнения (112) для функции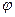 
с граничным условием (113) на контуре L поперечного сечения. Предложенный метод решения называется полуобратным методом Сен-Венана, в котором часть искомых величин задаётся, а остальные неизвестные определяются из общих уравнений теории упругости при заданных статических граничных условий.
Можно вместо функции кручения 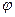ввести функцию напряжений F (x,y) Прандтля:
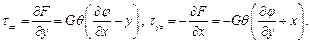(119)
В этом случае все три уравнения равновесия Коши будут тождественно удовлетворены. Составим гармоническую операцию над F.
С учётом (119) получаем:
(120)
Уравнение (120) называется уравнением Пуассона. Граничные условия:
,
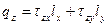с учётом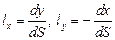 
(рис. 3.34) преобразуется к виду
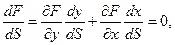
или
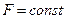(121)
на контуре L поперечного сечения.
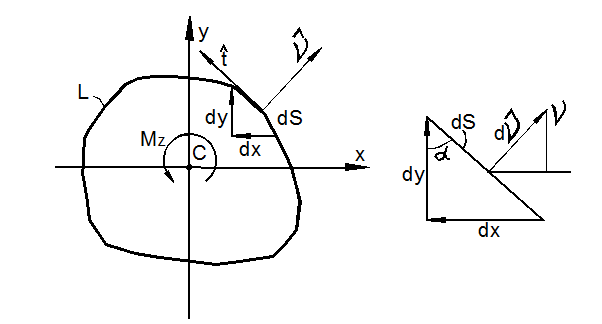
а) б)
Рис. 3.34
Крутящий момент (114) может быть представлен в виде
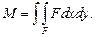(122)
Таким образом, задача о кручении в напряжениях сводится к нахождению функции напряжений F из уравнения Пуассона при граничном условии F = 0 на контуре поперечного сечения.
Date: 2015-05-22; view: 1030; Нарушение авторских прав