
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифференциальные уравнения равновесия Коши
|
|
Для равновесия тела необходимо и достаточно, чтобы каждая его частица находилась в равновесии. Выделим из тела материальную частицу в форме параллелепипеда со сторонами dx, dy, dz (рис. 3.32).
Действие отброшенной части тела заменим напряжениями, равномерно распределёнными по его граням. Напряжения на противоположных гранях могут отличаться на малые частные приращения вследствие приращения координат.
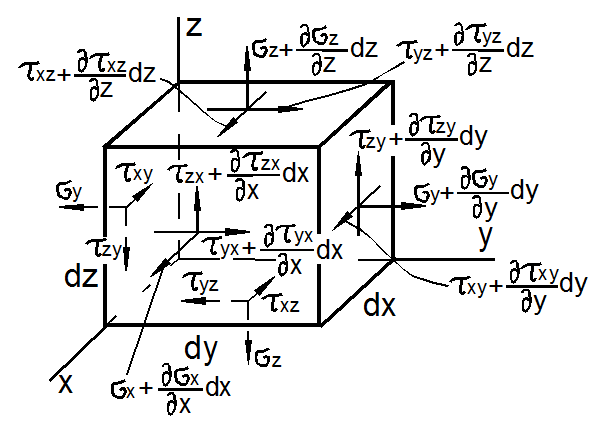
Рис. 3.32
Составим три уравнения равновесия в проекциях на оси x, y, z.
Проецируя все силы на ось х, получаем:
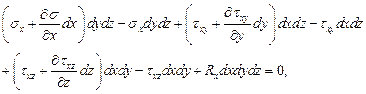
где 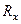 – проекция объёмной силы.
– проекция объёмной силы.
Аналогично можно записать уравнения равновесия в направлении осей y и z. После сокращений три уравнения равновесия Коши принимают вид:
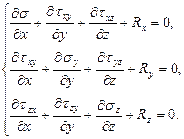 (100)
(100)
Составим ещё три уравнения равновесия моментов относительно осей x, y, z. Сумма моментов относительно оси х равна:
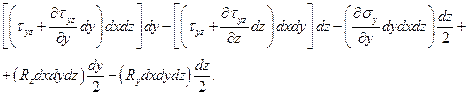
Аналогично можно записать ещё два уравнения равновесия моментов относительно осей y и z.
Сокращая на dxdydz и пренебрегая бесконечно малыми величинами высшего порядка, получаем закон парности касательных напряжений:
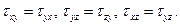 (101)
(101)
Система уравнений равновесия (100) Коши представляет собой дифференциальные уравнения равновесия в напряжениях. Они показывают с учётом (101), что задача определения напряжений трижды статически неопределима. При интегрировании уравнений (100) появятся произвольные функции, для определения которых используются статические граничные условия:
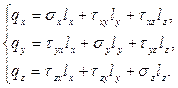 (102)
(102)
Иногда удобно иметь уравнения равновесия в перемещениях. Согласно закону Коши – Гука (21) и соотношений (83):
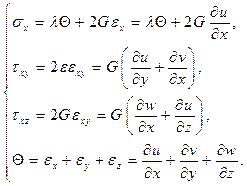 (103)
(103)
Подставляя (103) в первое уравнение (100), получим уравнение:
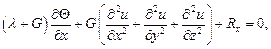
где
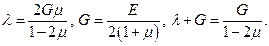
Аналогично получаются два других уравнения. В результате вместо (100) получаем систему уравнений Ламе в перемещениях:
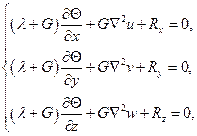 (104)
(104)
где
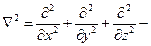
дифференциальный оператор Лапласа.
При интегрировании уравнений (104) используются геометрические граничные условия вида:
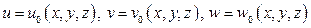
на поверхности тела 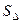 .
.
Date: 2015-05-22; view: 849; Нарушение авторских прав