Круги напряжений Мора

Удобное двумерное геометрическое представление трёхмерного напряжённого состояния было предложено немецким учёным О. Мором. Отнесём материальную частицу к главным осям (рис. 3.21). Рассечём её плоскостью, содержащей направление третьей главной оси (рис. 3.21,а). Тогда, согласно (35), имеем:

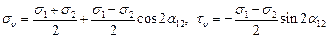(59)

Уравнения (59) представляют собой параметрические уравнения окружности, каноническое уравнение которой имеет в системе координат 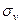, 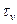вид (рис. 3.22):

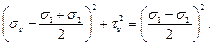(60)

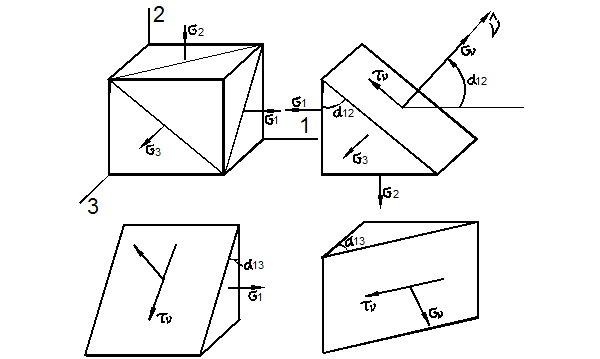
Рис. 3.21

Координаты центра окружности 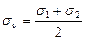, 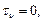радиус .

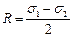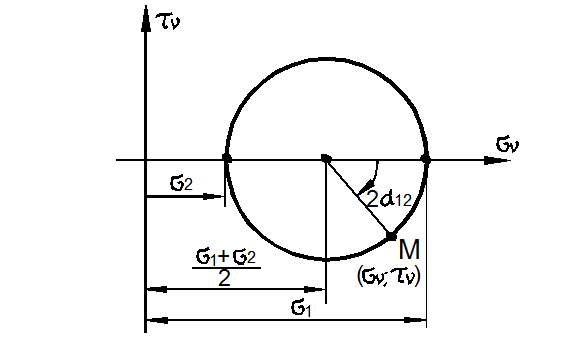
Рис. 3.22

Окружность Мора позволяет графически найти напряжение 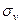, 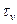на любой площадке, положение которой характеризуется углом 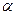. Для этого нужно отложить по часовой стрелке угол 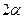и провести под этим углом радиус R до пересечения с окружностью в точке М. Координаты этой точки и есть искомое значения 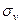, 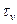. Наибольшее касательное напряжение возникает при 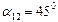и равно численно радиусу окружности Мора:

.

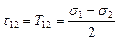Минимальное значение 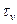возникает на площадке при и равно:

.

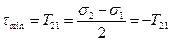Аналогичные круги Мора можно построить для наклонных площадок, содержащих главные направления 1 и 2 (рис. 3.23).

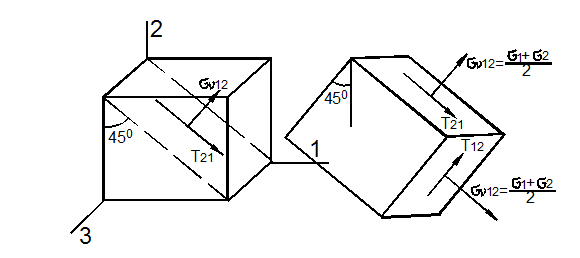
Рис. 3.23

Их уравнения в параметрической форме имеют вид:

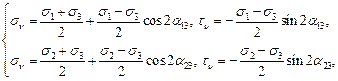
откуда следует, что наибольшее касательные напряжения в этих случаях:

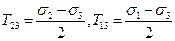
также равны радиусам соответствующих кругов Мора.

Касательные напряжения:

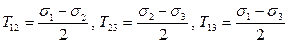(61)

носят название главных касательных напряжений. Они удовлетворяют тождеству

.

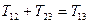Каждой точке на любой из окружности Мора отвечают напряжения 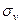, 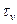и площадки, направление которой характеризуется одним из углов 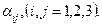Те площадки, которые не содержат ни одну из главных осей, окружностями Мора не описываются. Можно показать, что напряжения на этих площадках задаются точками, расположенными между окружностями в заштрихованной области. Из рис. 3.24 видно, что:

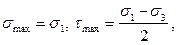(62)

если принято условие .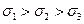

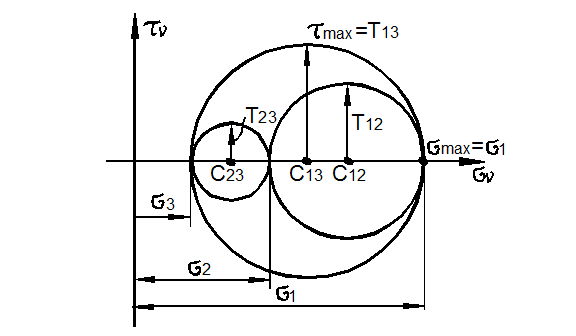
Рис. 3.24

Следовательно, 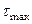определяется радиусом большого круга Мора. Величину

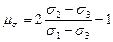(63)

называют параметром вида напряжённого состояния Лоде. При наложении на напряжённое состояние частицы всестороннего давления параметр Лоде не изменяется. Для одноосного растяжения 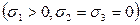имеем 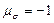, для сжатия 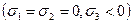имеем 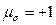, для плоского чистого сдвига 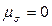. Соответствующие круги Мора приведены на рис. 3.25.

Таким образом, параметр Лоде 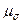характеризует вид напряжённого состояния.

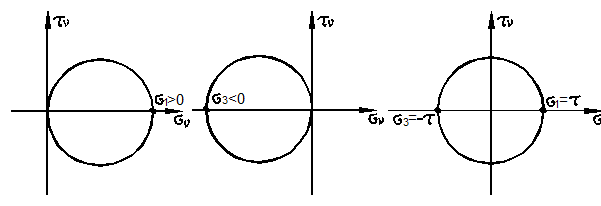
а) б) в)

Рис. 3.25

Если изначально напряжённое состояние не является двухосным, связанным с главными осями, то для построения круга напряжений Мора при плоском напряжённом состоянии следует использовать формулы (35):

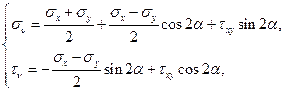(63)

Поступая так же, как и в случае двухосного растяжения сводим параметрические уравнения окружности (63) к каноническому виду (рис. 3.26):

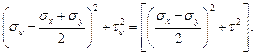(64)

В (64) мы имеем более сложное выражение радиуса окружности:

.

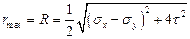При 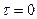уравнение (64) сводится к (60) как частному случаю.

При 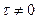построение круга Мора показано на рис. 3.26. Сначала определяется положение центра С круга как точки с координатами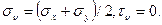

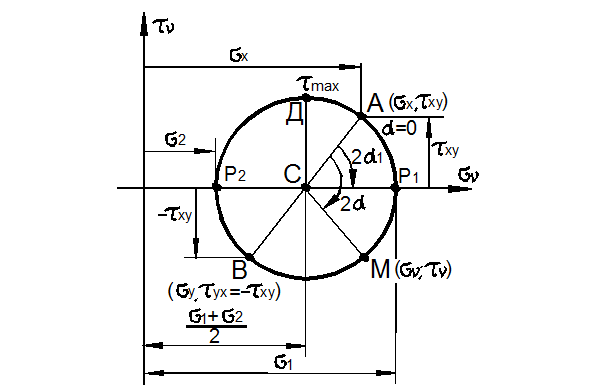
Рис. 3.26

Затем определяется положение точки А, характеризующей напряжения на грани элемента при 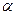=0, т.е. 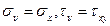. Здесь следует помнить правило знаков для 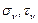и других напряжений, указанных на рис. 3.12. Заметим, что точки А и В, характеризующие напряжения на площадках, расположенных под углом 90⁰ друг к другу, лежат на противоположных концах диаметра круга Мора. Далее на АВ с центром в точке С чертится круг. Напряжения 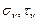на произвольной площадке, лежащей под углом 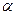к оси , можно определить следующим образом. Откладываем от точки А по часовой стрелке угол 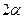и определяем положение точки М на круге с искомыми координатами 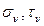. Точка М’, диаметрально противоположная Д, даёт напряжения 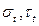для площадки, составляющей угол 90⁰ с той, которая имеет нормаль 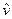, т.е. для площадки с углом 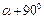с осью . Точка Д даёт максимальное касательное напряжение, равное радиусу круга Мора:

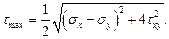(65)

Одной из важных задач использования круга Мора является определение главных нормальных напряжени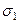й и 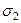. Этим напряжениям отвечают точки Р₁ и Р₂ круга. Из рис. 3.26 следует, что угол между направлениями на точки А и Р₁ равен удвоенному углу 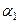, определяющему первое главное напряжение, а угол между направлениями А и Р₂ – удвоенный угол 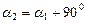, определяющий второе главное направление. Имеет место соотношение

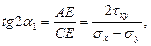
которое совпадает с формулой (36).

Из изложенного следует, что круг Мора можно использовать в качестве графического способа определения как напряжений на произвольной площадке, так и главных нормальных и максимальных касательных напряжений.

Date: 2015-05-22; view: 2058; Нарушение авторских прав