Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать неотразимый комплимент
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Главные нормальные напряжения и направления в общем случае объёмного напряжённого состояния
|
|
Плоские задачи являются частным случаем объёмного напряжённого состояния. Поставим задачу по определению таких площадок, на которых действуют только экстремальные нормальные напряжения, а касательные обращаются в нуль (рис. 3.17). Такие площадки назовём главными, а соответствующие экстремальные значения нормальных напряжений – главными нормальными напряжениями. Будем обозначать их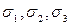 
и считать, что 
.
Направляющие косинусы нормали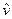 
на площадке общего положения удовлетворяют условию
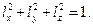(45)
Следовательно, возникает задача об отыскании условного экстремума напряжения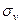 
при дополнительном условии (45).
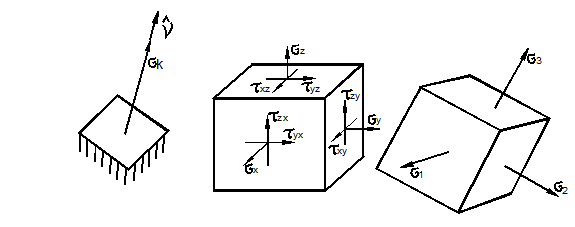
Рис. 3.17
Составим функцию Лагранжа:
,
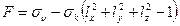где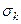 
играет роль неопределённых множителей Лагранжа. Найдём безусловный экстремум функции F по переменным 
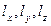. Для этого найдём частные производные по этим переменным и приравняем их к нулю:
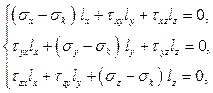(46)
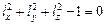. (47)
Так как 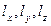одновременно обратиться в нуль не могут, то система трёх однородных алгебраических уравнений (46) имеет заведомо отличные от нуля решения.
В этом случае определитель системы (46) должен равняться нулю:
(48)
Раскрывая определитель (48), приходим к кубическому уравнению для определения трёх главных напряжений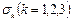 
:
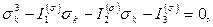(49)
где коэффициенты:
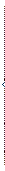
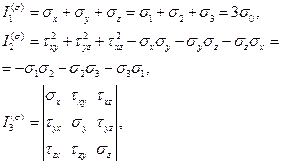(50)
являются инвариантамитензора напряжений по отношению к преобразованиям координат x, y, z. Все три корня уравнения (49) позволяют найти направляющие косинусы главных направлений напряжённого состояния частицы тела. Поскольку из трёх уравнений (46) только два независимы, то беря, например, два первых уравнения и решая их совместно с (47) относительно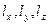 
по методу Крамера, получим:
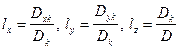
где
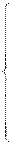
(51)
В частном случае плоской задачи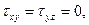 
и определитель (48) приводит к уравнению
откуда находим ранее полученную формулу
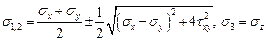
Полагая в (46)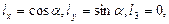 
получим систему уравнений:
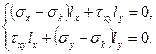
Умножая первое уравнение на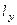 
, а второе на 
и вычитая, находим:
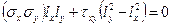
откуда, с учётом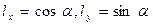 
, получим уже известную нам формулу (43):
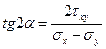
для определения углов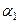 
, 
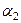, характеризующих направление главных осей.
Date: 2015-05-22; view: 400; Нарушение авторских прав