Пример 8

Пусть трехопорная балка (рис.20.13, а) нагружена силой величи­ной Р. Эта балка один раз статически неопределимая. На рис.20.13, б изображена эпюра изгибающих моментов, при упругой стадии де­формирования. Для решения этой задачи применим статический способ.

Рис. 20.13

Значение силы 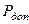, при которой в наиболее опасной точке балки напряжение достигает предела текучести, и может быть уста­новлено из равенства наибольшего момента, действующего в опас­ном сечении, допускаемому: 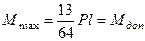. Откуда, полу­чим:

.

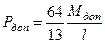Если балка имеет прямоугольное поперечное сечение, то

,

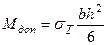и, следовательно,

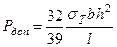. (20.33)

Наращивая величину внешней силы 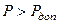, пластическая область в опасном сечении В балки увеличивается. При некотором значении силы в сечении В возникает пластический шар­нир, тогда величина изгибаю­щего момента в этом сечении становится равной 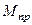. При дальнейшем росте внешней силы Р, момент в сечении В остается постоянным и равным 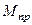. Это означает, что трех­опорная балка приобретает пластический шарнир в т. В. При этом она нагружена силой Р и двумя моментами 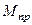, приложенных в разных торцах сечения В (рис.20.14, а). Следова­тельно, в данном случае возникновение одного пластического шар­нира превращает один раз статически неопределимую балку в балку статически определимую.

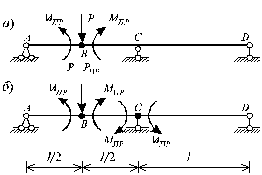
Рис. 20.14

При дальнейшем росте силы Р изгибающие моменты в сече­нии В и на участке АВ не возрастают, а изгибающие моменты на участке ВСD, с ростом величины силы Р, растут. При указанных предположениях, наибольшая величина изгибающего момента фор­мируется в сечении С, где он раньше всего и достигает предельной величины .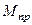

Когда в сечении С изгибающий момент достигнет предельной величины 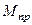, т.е. когда в этом сечении сформируется пласти­ческий шарнир, несущая способность балки исчерпается, вследствие чего, балка превращается в геометрически изменяемую систе­му.

Согласно статическому способу, и учитывая, что наиболее ве­роятная схема разрушения конструкции очевидна и изображена на рис.20.14, б, величина предельной силы определяется из уравнений равновесия и условий равенства изгибающего момента в сечениях пластического шарнира предельному моменту :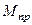

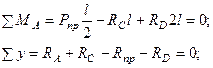
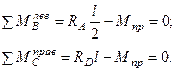
Решая совместно последнюю систему уравнений, получим:

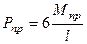, (20.34)

откуда:

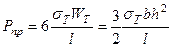. (20.35)

При расчете по методу допускаемых напряжений расчетная величина допускаемой силы определяется:

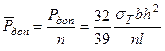, (20.36)

где n - коэффициент запаса по несущей способности конструкции.

В случае расчета по методу предельных состояний, величина допускаемой силы, принимает значение:

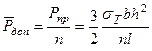. (20.37)

Сопоставляя выражения (20.36) и (20.37), получим, что метод рас­чета по предельному состоянию дает величину допускаемой силы в 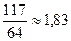раза больше, чем метод расчета по допускаемым напря­жениям, при условии, что коэффициент запаса в обоих методах принят одинаковым.

В заключении рассмотрим балку с одним защемленным, а вто­рым шарнирно опертым кон­цами, нагруженной двумя оди­наковыми силами (рис.20.15, а).

Рис. 20.15

Определим величину пре­дельной силы кинематиче­ским способом, предложен­ным А.А.Гвоздевым.

Рассматриваемая балка, один раз статически неопределима и, следовательно, ее несущая спо­собность исчерпается в случае образования двух пластических шарниров.

Пластические шарниры мо­гут формироваться в сечениях А, В и С. Для определения предельной нагрузки по кинематическому способу А.А.Гвоздева необходи­мо рассмотреть различные соче­тания образования пластических шарниров в двух сечениях из трех. Число таких комбинаций равно трем, т.е. числу сочетаний из трех пластических шарниров по два.

Для различных вариантов расположения пластических шарни­ров составляются уравнения равновесия, при условии равенства изгибающего момента в сечениях пластического шарнира предель­ному моменту 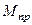. Из полученных уравнений могут быть опреде­лены величины предельных нагрузок. Действительной предельной нагрузкой будет наименьшая из вычисленных для различных соче­таний пластических шарниров.

Необходимо заметить, что при составлении уравнений предель­ного равновесия системы, можно использовать из трех уравнений статического равновесия всей системы в целом, только два из них. Третье уравнение автоматически будет удовлетворяться. Недостаю­щие уравнения могут быть получены, из рассмотрения равновесия отсеченной части системы, предполагая, что рассматриваемое сече­ние проходит через пластический шарнир.

Рассмотрим различные возможные схемы предельной стадии работы конструкции.

Первая схема, предполагая, что пластические шарниры фор­мируются в сечениях А и В (рис.20.15, б):

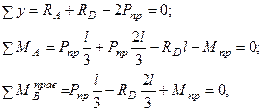
откуда 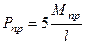. (20.38)

Вторая схема, предполагая, что пластические шарниры фор­мируются в сечениях А и С (рис.20.15, в):

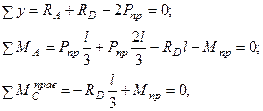
откуда 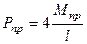(20.39)

Третья схема, предполагая, что пластические шарниры фор­мируются в сечениях В и С (рис.20.15, г):

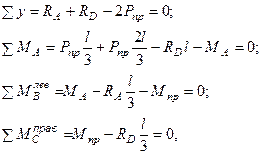
откуда, решая совместно эту систему уравнений, получим значения изгибающего момента в заделке 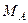и значение предельной нагруз­ки :

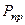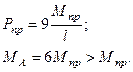(20.40)

Так как условие 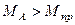не может быть реализовано, то третью схему следует исключить из дальнейшего рассмотрения.

Сопоставляя предельные значения внешней силы, приведенные в (20.38)-(20.39), определяем, что наименьшая предельная нагрузка имеет место при второй схеме предельного равновесия, т.е. когда пластические шарниры формируются в сечениях А и С:

.

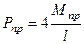Далее рассмот­рим применение кинематического способа - метода предельных сос­тояний для опре­деления величин продольных сил. Действительная схема разрушения системы показана на рис.20.16. Составим уравнения работ всех внутренних и внешних усилий на возможных перемещениях:

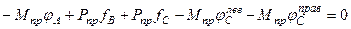. (20.41)

Составляя уравнения совместности, получим:

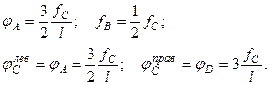(20.42)

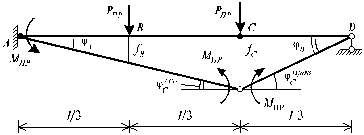
Рис. 20.16

Уравнение (20.41), с учетом (20.42), примет вид:

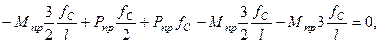
откуда 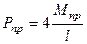. (20.43)

Сопоставляя выражения (20.43) и (20.39), заметим, что кинемати­ческий и статический способы дали идентичные результаты по зна­чению предельной силы.

Date: 2015-05-22; view: 697; Нарушение авторских прав