Капельная модель ядра

Одной из задач ядерной физики является объяснение эксперименталь­но установленной зависимости удельной энергии связи е нуклонов в ядре от массового числа А. Удовлетворительное объяснение этой зависимо­сти можно получить при помощи капельной модели ядра. Согласно этой модели под действием ядерных сил нуклоны в ядре расположены так близко друг к другу, что ядро становится похожим на каплю жидкости. Найдем зависимость радиуса R ядра от массового числа А. Пусть v -объем одного нуклона. Если представить себе ядро как шар из плотно прилегающих друг к другу нуклонов, то его объем будет приближенно равен произведению числа нуклонов в ядре на объем одного нуклона:

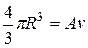
И.з этого равенства вытекает соотношение

R ~ А ^1/3 (23.18)

которое согласуется с результатами измерений радиусов атомных ядер. Пусть 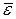е есть средняя энергия связи одного нуклона в ядре, обусло­вленная действием ядерных сил. Эту величину будем считать одинако­вой для всех ядер. Таким образом, в первом приближении энергия связи будет

E_cв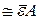

Е_св~ёА. (23.19)

Эту формулу можно сделать более точной следующим образом. Нукло­ны, расположенные у поверхности ядра, имеют в своем окружении мень­шее число частиц, чем нуклоны внутри ядра. Поэтому эти поверхност­ные нуклоны слабее связаны с ядром и энергия связи, приходящаяся на один такой нуклон, должна быть более низкой. Таким образом, среднюю энергию связи (23.19) следует уменьшить на величину, пропорциональ­ную числу поверхностных нуклонов, которое, в свою очередь, пропорцио­нально площади поверхности ядра. В силу зависимости (23.18) площадь поверхности ядра

4 π R ² ~ A ^2/3

В результате получим более точную формулу

E_cв = 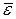A – k ₁ A ^2/3, (23.20)

где k ₁ - коэффициент пропорциональности. Эту формулу также можно уточнить, если еще учесть энергию кулоновского отталкивания протонов. Энергия взаимодействия двух протонов определяется выражением

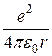
где r - расстояние между этими протонами. Потенциальная энергия вза­имодействия всех Z протонов ядра равна произведению средней энергии взаимодействия пары протонов на число

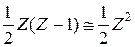
пар протонов в ядре. Так как среднее расстояние между протонами пропорционально радиусу R ядра, энергия кулоновского взаимодействия протонов будет пропорциональна выражению

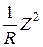~ A ^5/3

где учтено, что для стабильных ядер

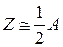
Кулоновское отталкивание протонов делает ядро менее устойчивым и уменьшает энергию связи. Поэтому с учетом энергии кулоновского вза­имодействия протонов выражение (23.20) следует изменить так, чтобы энергия связи стала

E_cв = 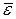A – k ₁ A ^2/3 – k ₂ A ^5/3 (23.21)

где k ₂ - еще один коэффициент пропорциональности. Эта формула при­водит к зависимости удельной энергии связи нуклонов в ядре от массо­вого числа

ε (A) = 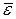- k ₁ A ^-1/3 – k ₂ A ^2/3 (23.22)

которая качественно правильно описывает аналогичную эксперимен­тальную зависимость ε = ε (A).

Date: 2015-05-19; view: 602; Нарушение авторских прав