Волновая функция

Состояние микрочастиц в квантовой механике описывается с помощью, так называемой, волновой функции вида ψ = f(x,y,z,t). Ее называют еще ψ-функция. Квадрат модуля ψ-функции определяет вероятность обнаружения частицы в момент времени t в области с координатами: x и x + d x; y и y + d y; z и z + d z – т.е. в элементе объема dV = d x d y d z:

dW = | ψ |² dV. (10)

Величина | ψ |² = dW /dV – имеет смысл плотности вероятности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестностях точки с координатами x,y,z. Т.о. физический смысл имеет не сама ψ-функция, а квадрат её модуля – |ψ|², которым и задается интенсивность волн де Бройля. Теперь вероятность найти частицу в момент времени t в объеме V будет:

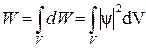. (11)

Очевидно, что объективность существования частицы во времени и в пространстве будет выражаться вероятностью достоверного события:

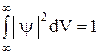. (12)

Это соотношение является условием нормировки ψ- функции.

Волновая функция позволяет рассчитать вероятность реализации тех или иных значений параметров микрообъекта или их средние величины, например, расстояние электрона от ядра атома или вероятность перехода электрона с одного энергетического уровня на другой, что в свою очередь позволяет оценить относительную интенсивность спектральных линий.

Что бы ψ-функция являлась объективной характеристикой состояния микрочастицы она должна удовлетворять следующим условиям: быть 1) конечной, т.к. W ≤ 1; 2) однозначной, т.к. вероятность не может быть неоднозначной; 3) непрерывной, т.к. вероятность не может изменяться скачком.