Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Из первого уравнения находим
|
|
.
Второе уравнение есть стационарное уравнение Шредингера
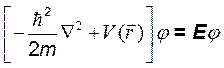. (4.5)
Пусть оператор энергии (гамильтониан)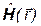 
имеет собственные функции 
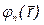и собственные значения Еn. Тогда в окончательном виде решение уравнения Шредингера для стационарных состояний имеет вид
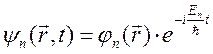. (4.6)
Отсюда следует, что состояния с определённым значением энергии Еn гармонически зависят от времени с частотой wn=En /ћ. Такие состояния называются стационарными. Для них важным является тот очевидный факт, что вероятность местоположения частицы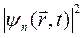 
и средние величины 
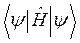не зависят от времени!
Уравнения Шредингера вида (4.4) и (4.5) описывают одну квантовую частицу в некотором поле с потенциалом V(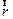
,t). Если квантовая система имеет много частиц, но взаимодействие между ними не учитывается, то в силу линейности гамильтониана и принципа суперпозиции уравнение Шредингера не изменяется, а волновая функция, как вероятностная характеристика независимых событий, определяется произведением всех одночастичных функций. Если учитывается взаимодействие между частицами, то потенциал взаимодействия должен зависеть от координат взаимодействующих частиц, т.е. V = V (
, 
,..., 
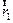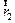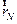,t), а оператор кинетической энергии должен быть суммой одночастичных операторов. Тогда уравнение Шредингера, например (4.5), принимает вид
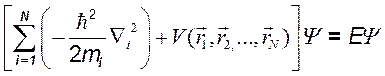, (4.7)
где операторы Ñ i действуют на координаты i -й частицы.
Рассмотрим свободное одномерное движение частицы (V =0). Для его описания будем решать уравнение Шредингера (4.5) с начальным условием
.
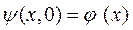Гамильтониан задачи не содержит потенциальной функции и имеет вид
.
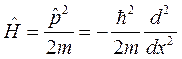Поскольку гамильтониан не зависит от времени, то достаточно найти решение стационарного уравнения Шредингера только для координатной части волновой функции j (х),
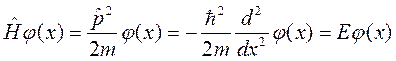(4.8)
а зависимость волновой функции от времени определяется формулой (4.6). Так как операторы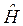 
, 
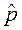и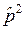 
коммутируют, то они имеют общую систему собственных функций. Прямой подстановкой легко проверить, что координатная часть волновой функции Де Бройля (1.13), являющаяся собственной функцией оператора 
,
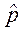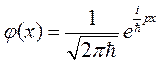
удовлетворяет уравнению (4.8) при непрерывном собственном значении
.
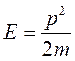Тогда частное решение уравнения Шредингера – это волна Де Бройля
,
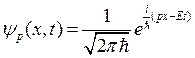а общее решение – это суперпозиция всех частных решений (возможных состояний):
.
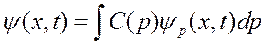Таким образом, волновая функция свободной частицы есть ни что иное, как «волновой пакет».
Date: 2015-05-19; view: 384; Нарушение авторских прав