ЛЕКЦИЯ №4

Уравнение Шредингера

Как известно, классическая механика родилась после формулирования уравнений динамики Ньютона, теория относительности приняла законченную форму после построения А.Эйнштейном общей теории относительности, описывающей динамику релятивистских частиц. Так и квантовая механика родилась после формулирования Шредингером в 1926 г. динамического уравнения для нерелятивистских квантовых частиц. Часто уравнение Шредингера называют пятым постулатом квантовой механики, но все-таки оно не было угадано, и для его формулировки существуют определенные физические основания.

Пусть известно значение волновой функции y(х, t) в момент времени t =0, т.е. y (х,0 )^~. Так как волновая функция полностью характеризует поведение частицы, то она должна определять и ее поведение в любые другие моменты времени, т.е. из волновой функции y (х,0 ) должна однозначно определяться функция y (х, t). Рассмотрим функцию y (х,D t) в момент времени D t, бесконечно мало отличающийся от нуля. Тогда

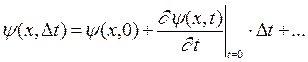
Согласно сказанному, коэффициент при D t должен определяться из y (х,0):

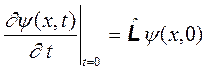, (4.1)

где 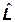– некоторый оператор, действующий на y (х,0). Оператор 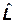осуществляет смещение во времени и должен быть найден из основных квантовых положений. Для определения его явного вида рассмотрим волновую функцию свободно движущейся частицы с определенным импульсом 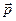. Для такого движения волновая функция совпадает с волной Де Бройля (1.7). Получим для нее явный вид оператора смещения во времени :

,

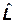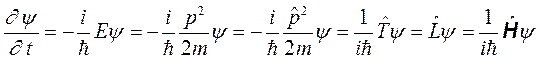где введен оператор

,

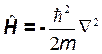являющийся результатом квантования функции Гамильтона

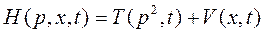
и для свободного движения частицы совпадающего с оператором кинетической энергии 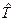. В общем случае при наличии потенциального поля V гамильтониан

будет иметь вид:

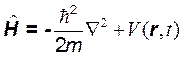. (4.2)

Таким образом, для свободного движения оператор смещения во времени имеет вид:

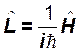. (4.3)

В квантовой механике постулируется, что

оператор смещения во времени всегда (для любого движения) выражается через гамильтониан по формуле (4.3).

Тогда окончательно уравнение для волновой функции записывается следующим образом:

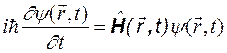. (4.4)

Это уравнение называется уравнением Шредингера. В отсутствие переменных внешних полей гамильтониан 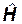не зависит от времени. В этом случае в уравнении Шредингера можно провести разделение переменных. Представим волновую функцию в виде 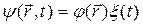, подставим ее в (4.4), разделим переменные и, обозначив постоянную разделения через Е, получим уравнения

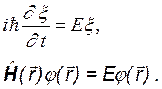
Date: 2015-05-19; view: 358; Нарушение авторских прав