Уравнение Шредингера. Микрочастицы обладают волновыми свойствами, поэтому классическая механика не может дать правильного описания их поведения

Микрочастицы обладают волновыми свойствами, поэтому классическая механика не может дать правильного описания их поведения. Квантовая механика создана Э.Шредингером, В. Гайзенбергом, П. Дираком и другими учеными. Основное уравнение нерелятивистской квантовой механики в 1926 году сформулировано Э. Шредингером.

Нестационарное (общее) уравнение Шредингера:

,

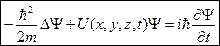где 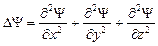– оператор Лапласа (записан в декартовых координатах); 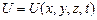– потенциальная энергия частицы в силовом поле; 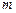– масса микрочастицы; 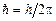; 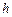– постоянная Планка; – мнимая единица. Уравнение справедливо для любой частицы, движущейся с малой (по сравнению со скоростью света) скоростью.

Рассмотрим свободно движущуюся частицу, которой, согласно идее де Бройля, сопоставляется плоская волна. Уравнение плоской волны, распространяющейся вдоль оси 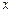, имеет вид:

.

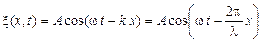Это выражение в комплексном ви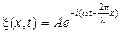де: , где 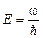– полная энергия частицы; 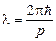– длина волны; 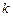– волновое число.

Получим для одномерного случая свободно движущейся частицы волновую функцию:

.

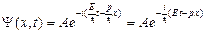Зависимость энергии от импульса:

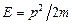. (26)

Дифференцируя функцию один раз по 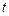и дважды по 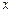, получаем:

; .

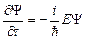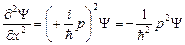Из этих соотношений найдем 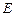и 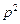через функцию и ее производную:

, .

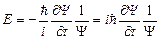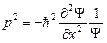Подставляя эти выражения в (26), получаем дифференциальное уравнение:

.

Если направление волны не совпадает с осью 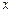, фаза колебаний будет зависеть от координат (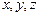). Для этого случая уравнение имеет вид:

.

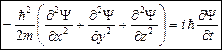Учитывая (26), получаем стационарное уравнение для свободной частицы:

.

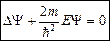Это уравнение совпадает с уравнением Шредингера для случая 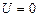, так как мы рассматривали свободную частицу.

Если частица движется в силовом поле, характеризуемом потенциальной энергией 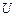, то полная энергия 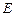складывается из кинетической и потенциальной энергий.

Полная энергия микрочастицы:

,

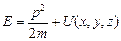где 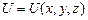и не зависит явно от времени.

Уравнение Шредингера для стационарных состояний:

.

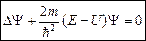Date: 2015-05-19; view: 435; Нарушение авторских прав