Гипотеза Луи де Бройля

Французский физик Луи де Бройль в 1924 году выдвинул гипотезу об универсальности корпускулярно-волнового дуализма. Он утверждал, что не только фотоны, но и электроны и любые элементарные частицы наряду с корпускулярными обладают также волновыми свойствами.

По де Бройлю, с каждым микрообъектом связываются характеристики: корпускулярные – энергия 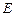и импульс 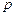; волновые – частота 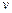и длина волны 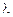. Однако электроны и большинство других элементарных частиц имеют массу покоя, а фотоны «в покое» не существуют.

Любой микрочастице, обладающей импульсом 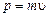, сопоставляют волну, длина которой вычисляется по формуле де Бройля. Длина волны де Бройля:

,

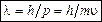где 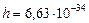Дж×с – постоянная Планка; 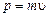– импульс частицы.

Гипотеза де Бройля была подтверждена экспериментально.

В 1927 году американские физики К. Девиссон и Л. Джермер обнаружили, что пучок электронов, рассеивающийся от естественной дифракционной решетки (кристалл никеля) дает отчетливую дифракционную картину, аналогичную той, которая имеет место от рентгеновских лучей. Дифракционные максимумы соответствовали формуле Вульфа – Брэгга, а длина волны оказалась равной длине волны, вычисленной по де Бройлю.

Советский ученый П. Тартаковский наблюдал дифракционную картину при прохождении пучка быстрых электронов через металлическую фольгу.

О. Штерн и его сотрудники показали, что дифракционные явления обнаруживаются также у атомных, молекулярных и нейтронных пучков.

Таким образом, микрочастицы обладают волновыми свойствами.

Соотношение неопределенностей

В классической механике всякая частица движется по определенной траектории, так что в любой момент времени точно фиксированы ее координата и импульс. Микрочастицы ввиду наличия у них волновых свойств не имеют траектории, и неправомерно говорить об одновременных точных значениях ее координаты и импульса.

В. Гейзенберг, учитывая волновые свойства микрочастиц, пришел в 1927 году к выводу, что объект микромира невозможно одновременно с одинаковой степенью точности характеризовать его координатой и импульсом.

Согласно соотношению неопределенностей Гейзенберга, микрочастица не может иметь одновременно определенные координату (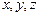) и соответствующую проекцию импульса (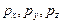), причем неопределенности в значениях этих величин удовлетворяют условиям:

, ,

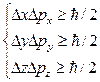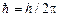где 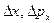, , 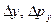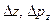- соответственно неопределенности координат и импульсов.

В квантовой теории рассматривается соотношение неопределенностей для энергии 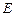и времени 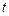, т.е. неопределенности в значениях этих величин удовлетворяют условию:

.

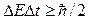Следовательно, система, имеющая среднее время жизни 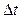, не может быть охарактеризована определенным значением энергии. Разброс значений энергии 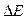возрастает с уменьшением среднего времени жизни.

Так как в классической механике принимается, что измерение координаты и импульса может быть произведено с любой точностью, то соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.

Волновая функция

и ее статистический смысл

Квантовая механика описывает законы движения и взаимодействия микрочастиц с учетом их волновых свойств.

Согласно волновым представлениям о природе света, интенсивность дифракционной картины пропорциональна квадрату амплитуды световой волны. С точки зрения корпускулярной теории интенсивность определяется числом фотонов, попадающих в данную точку дифракционной картины. Следовательно, дифракционная картина для микрочастиц является проявлением статистической (вероятностной) закономерности, согласно которой частицы попадают в те места, где интенсивность волн де Бройля наибольшая.

В квантовой механике состояние микрочастицы описывается волновой функцией 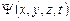. Квадрат модуля волновой функции определяет вероятность нахождения частицы в момент времени 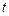в элементе объема 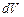. 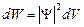, отсюда 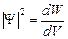- имеет смысл плотности вероятности.

Вероятность найти частицу в момент времени 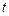в конечном объеме 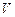равна .

Если объем равен бесконечности, т.е. частица находится где-то в пространстве, то выполняется условие нормировки вероятности:

,

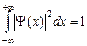
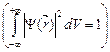где 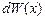– вероятность того, что частица может быть обнаружена вблизи точки с координатой 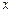на участке 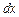; 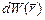- вероятность обнаружения микрочастицы в объёме .

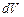Свойства волновой функции:

– Функция характеризует вероятность обнаружения микрочастицы в элементе объема, поэтому должна быть конечной.

– Функция должна быть однозначной, так как вероятность не может быть неоднозначной величиной.

– Функция должна быть непрерывной, так как вероятность не может изменяться скачком.

– Функция удовлетворяет принципу суперпозиции (если система может находиться в различных состояниях, описываемых волновыми функциями 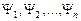, то она также может находиться в состоянии , описываемом линейной комбинацией этих функций: ).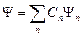

Date: 2015-05-19; view: 701; Нарушение авторских прав