Среднее значение величины

Пусть частица находится в состоянии Ψ, являющемся суперпозицией собственных функций некоторого оператора 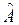. Такие функции образуют ортонормированный базис 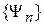, как доказано в (2.16). В состоянии Ψ физическая величина A не имеет определенного значения. Получим ее среднее значение.

Разложение состояния Ψ по базису .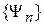

Дискретный спектр

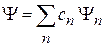. (2.23)

Непрерывный спектр

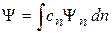. (2.24)

Установим смысл коэффициентов разложения .

Коэффициенты разложения . Умножаем (2.23) или (2.24) на , интегрируем по пространственным переменным, переставляем суммирование и интегрирование, учитываем условия ортонормированности (2.21) или (2.22). Для дискретного спектра

,

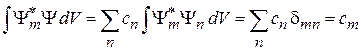для непрерывного спектра

.

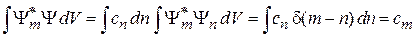Заменяем 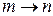и для дискретного и непрерывного спектров находим

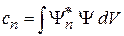. (2.25)

Подставляем разложение функции (2.23) 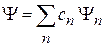в условие нормировки (1.16) 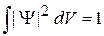. Для дискретного спектра получаем

.

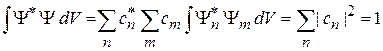Сравниваем результат с нормировкой вероятности дискретных событий

,

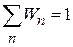следовательно, 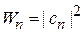. Вероятность обнаружения состояния 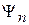в нормированном состоянии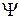

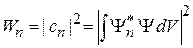. (2.26)

Для непрерывного спектра в условие нормировки

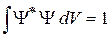
подставляем (2.24)

,

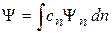учитываем (2.22)

,

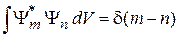получаем

.

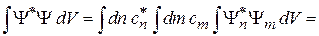
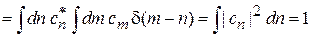Сравниваем результат с нормировкой вероятности непрерывных событий

,

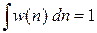следовательно, 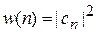. Плотность вероятности обнаружения состояния 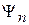в нормированном состоянии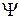

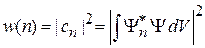. (2.27)

Среднее значение величины, описываемой оператором 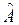, в нормированном состоянии 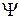, равно

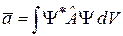. (2.28)

Доказательство:

Состояние разлагаем по собственным функциям оператора с дискретным спектром

,

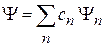подставляем в (2.28), учитываем

,

,

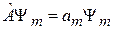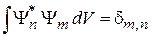получаем

.

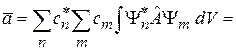
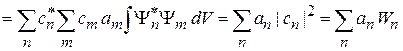Результат совпадает с определением среднего в теории вероятности дискретной величины.

Для непрерывной величины аналогично находим известное в теории вероятности выражение

.

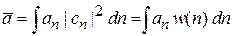Date: 2015-05-19; view: 458; Нарушение авторских прав