ВОЛНОВАЯ функция

МАТЕМАТИЧЕСКИЕ ОСНОВЫ КВАНТОВОЙ МЕХАНИКИ

Квантовая механика, не ограниченная полуклассическим приближением, строится на совершенно другом основании, чем классическая физика. Состояние частицы описывается функцией, множество состояний образует гильбертого пространство функций. Измеряемая физическая величина описывается линейным оператором, действующим в гильбертовом пространстве.

Основные положения:

Состояние частицы описывается волновой функцией.

Физическая величина описывается оператором.

Собственные значения оператора являются возможными результатами измерения величины. Разложение волновой функции по ортонормированному базису собственных функций оператора дает вероятности возможных результатов измерения соответствующей физической величины.

Волновая функция и энергия частицы получаются в результате решения уравнения Шредингера.

Квантовая механика в общем случае не дает однозначных результатов для характеристик частицы, но лишь вероятности тех или иных результатов, которые удовлетворяют соотношениям неопределенностей.

ВОЛНОВАЯ функция

Состояние частицы выражает комплексная функция Y (пси), являющейся амплитудой вероятности обнаружения частицы:

.

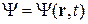Физический прибор – детектор частиц регистрирует 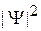. Физический смысл:

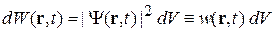
– вероятность обнаружения частицы в момент t в объеме 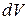около точки ;

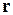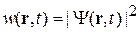
– плотность вероятности – вероятность обнаружения частицы в момент t в единичном объеме около точки r.

Условие нормировки

.

Волновая функция:

1) Определена с точностью до постоянного фазового множителя;

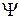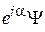состояния и , где 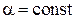, физически не различимы;

2) Квадратично интегрируема, 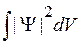– существует;

3) Удовлетворяет принципу суперпозиции – если возможны состояния 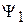и 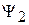, то возможно состояние

,

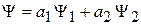где – комплексные числа, определяющие вероятность обнаружения состояний 1 и 2.

Date: 2015-05-19; view: 405; Нарушение авторских прав