Задачи для самостоятельного решения. 3.1. Найти длину волны: 1) электрона, летящего со скоростью 108см/с; 2) атома водорода, движущегося со скоростью

3.1. Найти длину волны: 1) электрона, летящего со скоростью 10⁸см/с; 2) атома водорода, движущегося со скоростью, равной средней квадратичной скорости при температуре 300К; 3) шарика массой 1 г, движущегося со скоростью 1 см/с.

3.2. Найти длину волны де Бройля для электрона, прошедшего разность потенциалов U₁=1B; U₂=100 B.

3.3. Решить предыдущую задачу для пучка протонов.

3.4. Электрон, движущийся со скоростью 5000 км/с, попадает в однородное ускоряющее поле напряженностью 10 В/см. Какое расстояние должен пройти электрон в поле, чтобы длина волны де Бройля стала равной 1 ангстрему?

3.5. Вычислить длину волны де Бройля l для протона, движущегося со скоростью u = 0,6 с (с – скорость света в вакууме).

3.6. Найти длину волны де-Бройля для электрона, кинетическая энергия которого равна 1) 10 эВ, 2) 1 МэВ.

3.7. Заряженная частица, ускоренная разностью потенциалов 200 В, имеет длину волны де-Бройля 2,02 пм. Найти массу частицы, если известно, что заряд ее численно равен заряду электрона.

3.8. Составить таблицу значений длин волн де Бройля для электрона, движущегося со скоростью, равной 2.10⁸; 2,2.10⁸, 2,4.10⁸; 2,6.10⁸; 2,8.10⁸ м/с.

3.9. Скорость так называемых тепловых нейтронов, средняя кинетическая энергия которых близка к средней энергии атомов газа при комнатной температуре, 2,5 км/с. Найти длину волны для таких нейтронов.

3.10. В телевизионной трубке проекционного аппарата электроны разгоняются до скорости 10⁸ м/с. Определить длину волны катодных лучей без учета и с учетом зависимости массы от скорости.

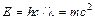3.11. а) Чему равна релятивистская масса электрона, длина которого 0,0420 ? б) Из соотношения можно найти эффективную массу фотона (). Чему равна эффективная масса фотона, длина волны которого 0,0420 .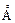

3.12. a-частица движется по окружности радиусом 8б3 мм в однородном магнитном поле, напряженность которого 18,9 кА/м. Найти длину волны де-Бройля для a-частицы.

3.13. Найти длину волны де Бройля для a-частицы, нейтрона и молекулы азота, движущихся со средней квадратичной скоростью при температуре 25^оС.

3.14. Поток летящих параллельно друг другу электронов, имеющих скорость v=10⁶ м/с, проходит через щель ширины b=0,1 мм. Найти ширину центрального дифракционного максимума, наблюдаемого на экране, отстоящем от щели на расстоянии l =10 см.

3.15. Узкий пучок монохроматических электронов падает нормально на поверхность монокристалла никеля. В направлении, составляющем угол в 55^о с нормалью к поверхности, наблюдается максимум отражения четвертого порядка при энергии электронов Е_к=180 эВ. Вычислить соответствующее значение межплоскостного расстояния.

3.16. На грань некоторого кристалла под углом 60^о к ее поверхности падает параллельный пучок электронов, движущихся с одинаковой скоростью. Определить скорость электронов, если они испытывают интерференционное отражение первого порядка. Расстояние между атомными плоскостями кристалла равно 0,2 ни.

3.17. Пучок нейтронов, получаемых в результате ядерной реакции, падает на кристалл с периодом решетки 1.5 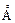. Определите скорость нейтронов, если брэгговское отражение первого порядка наблюдается, когда угол скольжения равен 30^о.

3.18. На грань кристалла никеля падает под углом 64^о к поверхности грани параллельный пучок электронов, движущихся с одинаковой скоростью. Принять расстояние между соответствующими плоскостями, параллельными грани кристалла, d=200 пм. Пользуясь уравнением Вульфа-Брегга, найти скорость электронов, если они испытывают интерференционное отражение 1-го порядка.

3.19. Положение центра шарика с массой 10^-3 кг и положение электрона известно с точностью до 10^-4 м. Найти наименьшую ошибку, с которой при этом можно определить скорость шарика и скорость электрона.

3.20. Неопределенность скорости электронов, движущихся вдоль оси абсцисс, составляет Dv=10²м/с. Какова при этом неопределенность координаты х, определяющей местоположение электрона?

3.21. Молекулы водорода участвуют в тепловом движении при Т=300 К. Найти неопределенность координаты Dх молекул водорода.

3.22. Неточность в определении местоположения частицы, движущейся вдоль оси х, равна длине волны де Бройля для этой частицы. Найти относительную неточность в определении ее скорости.

3.23. Неточность при измерении координаты электрона, движущегося по прямолинейной траектории, равна 10 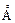. Рассчитайте неточность в определении: а) импульса; б) скорости; в) кинетической энергии этого электрона.

3.24. Время существования возбужденного состояния ядер имеет порядок 10¹²с. Какова неопределенность энергии DE квантов, испускаемых ядрами?

IV. Элементы квантовой механики.

1. Уравнение Шредингера для стационарных состояний:

,

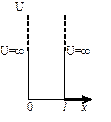
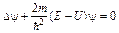где y – волновая функция, Е –полная энергия частицы, U – ее потенциальная энергия. D оператор Лапласа ().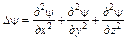

Для частицы, находящейся в бесконечно глубоком одномерном ящике решение уравнения Шредингера (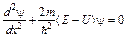) имеет вид:

,

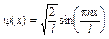где n=1,2,3,..., l –ширина ящика, х – координата (0<x< l).

Энергия частицы в потенциальной яме тоже оказывается квантованной и принимает значения:

,

где 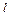- ширина ящика.

Для потенциальной ямы, форма которой определяется потенциальной энергией 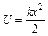, решение уравнения Шредингера имеет вид: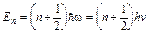

2. Если имеется потенциальный барьер, энергия которого выше полной энергии частицы, то существует вероятность обнаружить частицу за потенциальным барьером. В этом случае решение уравнения определяет коэффициент прозрачности барьера:

,

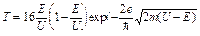где Е – полная энергия частицы, U – высота потенциального барьера.

Date: 2015-05-19; view: 2445; Нарушение авторских прав