Постулаты квантовой теории. Волновая функция (статистическая интерпретация волновой функции)

Детальный анализ процессов рассеяния электронов на атомах на основе уравнения Шрёдингера привел Борна (M. Born) к вероятностной интерпретации волновой функции частицы (1926 г.): квадрат модуля 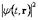есть плотность вероятности обнаружить частицу в точке пространства 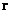в момент времени 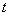. Таким образом, квантовая механика (даже для одной частицы) является вероятностной теорией, в которой принцип причинности отличается от соответствующего лапласовского принципа причинности в классической механике. В своей статье 1926 г. Борн так сформулировал основную особенность квантовой теории: «Движение частицы следует вероятностным законам, сама же вероятность распространяется в соответствии с законом причинности».

Указанная вероятностная интерпретация волновой функции – один из основных постулатов квантовой теории, который подтвержден всей совокупностью проведенных экспериментов.
Покажем, что из УШ вытекает закон сохранения вероятности. Запишем уравнения для 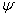и комплексно сопряженной к ней функции :

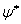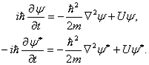
Умножив первое уравнение на 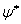, а второе на 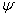, вычтем одно из другого. Получим

.

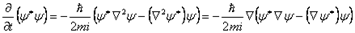Введем плотность 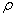и поток вероятности :

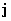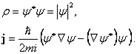
В результате находим уравнение непрерывности (ср. с электродинамикой, ч. 1 курса):

.
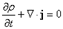Проинтегрировав его по объему 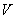, ограниченному замкнутой поверхностью 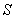, получим интегральный закон сохранения вероятности:

.

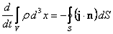Удалив 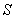в бесконечность, в предположении, что

,

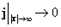получим

,

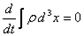или

.

Для физически реализуемых состояний всегда можно выбрать такую нормировку волновой функции, что

.

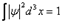Это соотношение означает, что вероятность обнаружить частицу во всем пространстве равна единице, как и должно быть.

Замечание. Плотность 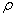и поток вероятности 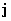инвариантны относительно преобразования фазы волновой функции:

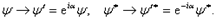
Функци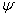и и отвечают одному и тому же состоянию.

48. Постулаты квантовой теории. Физическая величина – оператор

Каждой физической величине соответствует оператор этой физической величины. Оператор – это математическое правило, согласно которому можно преобразовать одну функцию в другую. Оператором физической величины может быть только линейный эрмитов (самосопряженный) оператор.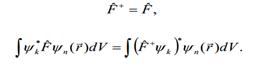

Значения, которые может принимать данная физическая величина называют ее собственными значениями. Если при действии оператора на функцию получается та же самая функция, умноженная на число, то есть 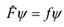то такую функцию называют собственной функцией оператора 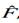, 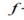– его собственное значение.

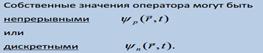
Спектр собственных значений эрмитова оператора вещественен.

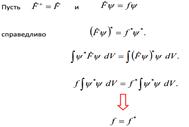
Date: 2015-05-19; view: 652; Нарушение авторских прав