Стационарное уравнение Шредингера. Стационарные состояния

Среди решений уравнения 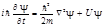,особый интерес представляют волновые функции вида 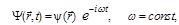описывающие состояния, называемые стационарными. Легко проверить, что волновая функция вида (Б.2) будет решением уравнения Шредингера уравнения 1, если 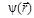удовлетворяет уравнению 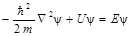где 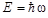. Постоянная E в уравнении 3 имеет смысл полной энергии частицы. Таким образом, в стационарных состояниях Е = соnst, а зависимость волновой функции 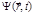от времени описывается сомножителем 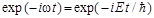, осциллирующим с частотой .

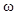Уравнение 3 называется уравнением Шредингера для стационарных состояний, или стационарным уравнением Шредингера. Существенно, что стационарное уравнение Шредингера имеет физически приемлемые решения, вообще говоря, не для любых значений Е, а лишь для некоторого множества 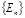. Находя такие решения, мы одновременно получаем и набор возможных значений энергии стационарных состояний электрона при заданных внешних условиях. О нахождении множества 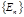говорят как об определении энергетического спектра, или уровней энергии, или как о квантовании энергии частицы. Физически приемлемыми в рассматриваемом круге задач считаются функции , однозначные и ограниченные во всей области их определения. Можно показать, что удовлетворяющие стационарному уравнению Шредингера (Б.3) однозначные ограниченные функции, будут непрерывными и гладкими (т.е. имеющими непрерывную первую производную) даже в тех точках, где 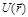претерпевает конечный разрыв (скачок).

Date: 2015-05-19; view: 433; Нарушение авторских прав