Гармонический осциллятор. В заключение рассмотрим задачу о колебаниях квантового гармонического осциллятора

В заключение рассмотрим задачу о колебаниях квантового гармонического осциллятора. Таким осциллятором являются частицы, совершающие малые колебания около положения равновесия.

На рис. 18.1, а изображен классический гармонический осциллятор в виде шарика массой m, подвешенного на пружине с коэффициентом жесткости k. Сила, действующая на шарик и ответственная за его колебания, связана с координатой х формулой 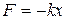. Потенциальная энергия шарика есть

.

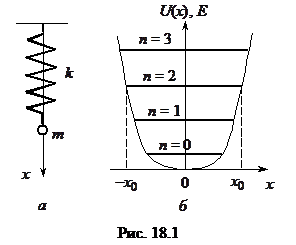
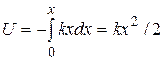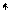Если шарик вывести из положения равновесия, то он совершает колеба­ния с частотой 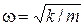. Зависимость потенциальной энергии от координа­ты х показана на рис. 18.1, б.

Уравнение Шредингера для гармонического осциллятора имеет вид

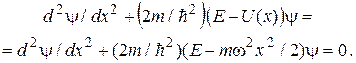
Решение этого уравнения приводит к квантованию энергии осциллятора. Собственные значения энергии осциллятора определяются выражением

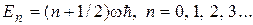
Как и в случае потенциальной ямы с бесконечно высокими стенками, минимальная энергия осциллятора 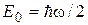отлична от нуля. Наименьшее возможное значение энергии при n = 0 называют энергией нулевых колебаний. Для классического гармонического осциллятора в точке с координатой x = 0 энергия равна нулю. Существование энергии нулевых колебаний подтверждается экспериментами по изучению рассеяния света кристаллами при низких температурах. Спектр энергий частицы оказывается эквидистантным, т. е. расстояние между уровнями энергии равно энергии колебаний классического осциллятора

.

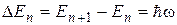При передаче энергии через фотон его частота оказывается равной w.

Приведем (без вывода) выражения для нескольких первых собственных функций гармонического осциллятора:

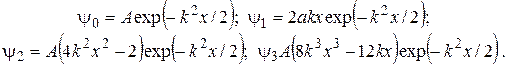
Графики для соответствующих плотностей вероятности изображены на рис. 18.2. Границы «классической» траектории осциллятора помечены как 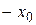и .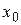

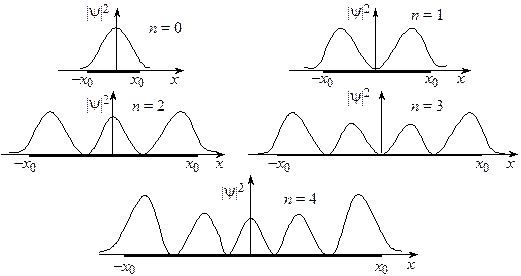
Рис. 18.2

Проведем сравнение с классическим случаем. Очевидно, что в этом случае вероятность 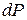нахождения частицы в интервале 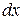обратно пропорциональна скорости частицы 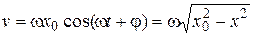, где 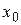есть точка поворота частицы при колебаниях, т. е. .

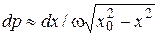График «классической» плотности вероятности изображен на рис. 18.3 пунктирной кривой. Видно, что, как и в случае потенциальной ямы, поведение квантового осциллятора существенным образом отличается от поведения классического.

Вероятность для классического осциллятора всегда максимальна вблизи точек поворота, а для квантового осциллятора вероятность максимальна в пучностях собственных Y-функций. К тому же квантовая вероятность оказывается отличной от нуля и за точками поворота, ограничивающими движение классического осциллятора.

На примере квантового осциллятора опять прослеживается упоминавшийся ранее принцип соответствия. На рис. 18.3 изображены графики для классической и квантовой плотностей вероятности при большом квантовом числе n. Хорошо видно, что усреднение квантовой кривой приводит к классическому результату.

ТЕПЛОВОЕ ИЗЛУЧЕНИЕ. КВАНТОВАЯ ОПТИКА

1. Тепловое излучение..................................................................................... 3

2. Закон Кирхгофа. Абсолютно черное тело............................................. 4

3. Закон Стефана – Больцмана и закон Вина. Формула Рэлея – Джинса. 6

4. Формула Планка..................................................................................... 8

5. Явление внешнего фотоэффекта............................................................ 10

6. Опыт Боте. Фотоны............................................................................... 12

7. Излучение Вавилова – Черенкова........................................................ 14

8. Эффект Комптона.................................................................................. 17

ОСНОВНЫЕ ПОЛОЖЕНИЯ КВАНТОВОЙ МЕХАНИКИ

9. Гипотеза де-Бройля. Опыт Дэвиссона и Джермера............................. 19

10. Вероятностный характер волн де-Бройля. Волновая функция......... 21

11. Принцип неопределенности................................................................ 24

12. Уравнение Шредингера....................................................................... 26

13. Частица в потенциальной яме............................................................. 30

14. Потенциальная яма конечной глубины.............................................. 32

15. Принцип соответствия в квантовой механике.................................... 35

16. Прохождение частицы через потенциальный барьер. Туннельный

эффект......................................................................................................... 36

17. Движение свободной частицы............................................................. 42

18. Гармонический осциллятор................................................................ 43

Малышев Михаил Николаевич, Павловская Мария Владимировна,

Попов Юрий Игоревич, Земцов Антон Валерьянович

Основы квантовой физики

Учебное пособие

Редактор Н. В. Рощина

ЛР № 020617 от 24.06.98.

Подписано в печать 00.09.2003. Формат 60´84 1/16. Бумага офсетная.

Печать офсетная. Гарнитура «Times». Усл. печ. л. 2,79. Уч.-изд. л. 3,0.

Date: 2015-05-18; view: 721; Нарушение авторских прав