Частица в потенциальной яме. Найдем собственные значения энергии и соответствующие им собственные волновые функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной

Найдем собственные значения энергии и соответствующие им собственные волновые функции для частицы, находящейся в бесконечно глубокой одномерной потенциальной яме (рис. 13.1, а). Предположим, что частица

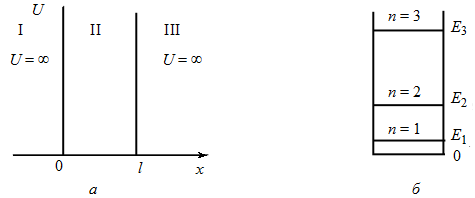
Рис. 13.1

может двигаться только вдоль оси х. Пусть движение ограничено непроницаемыми для частицы стенками: х = 0 и х = l. Потенциальная энергия U = 0 внутри ямы (при 0 £ х £ l) и 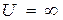вне ямы (при х < 0 и х > l).

Рассмотрим стационарное уравнение Шредингера. Поскольку Y-функ­ция зависит только от координаты х, то уравнение имеет вид

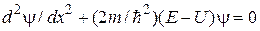. (13.1)

За пределы потенциальной ямы частица попасть не может. Поэтому вероятность обнаружения частицы вне ямы равна нулю. Следовательно, и функция y за пределами ямы равна нулю. Из условия непрерывности следует, что y должна быть равна нулю и на границах ямы, т. е.

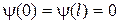. (13.2)

Этому условию должны удовлетворять решения уравнения (13.1).

В области II (0 £ х £ l), где U = 0 уравнение (13.1) имеет вид

.

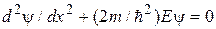Используя обозначение 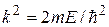, придем к известному из теории колебаний волновому уравнению

.

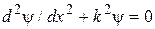Решение такого уравнения имеет вид

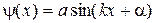. (13.3)

Условию (14.2) можно удовлетворить соответствующим выбором постоянных k и a. Из равенства 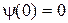получаем 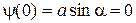Þ a = 0.

Далее из равенства 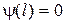получаем 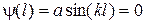. Это условие выполняется при

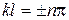(n = 1, 2, 3,...), (13.4)

n = 0 исключено, поскольку при этом 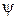º 0, т. е. вероятность обнаружения частицы в яме равна нулю.

Из (13.4) получаем 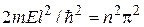(n = 1, 2, 3,...), следовательно,

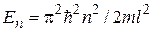(n = 1, 2, 3,...).

Таким образом получаем, что энергия частицы в потенциальной яме может принимать только дискретные значения. На рис.13.1, б изображена схема энергетических уровней частицы в потенциальной яме. На этом примере реализуется общее правило квантовой механики: если частица локализована в ограниченной области пространства, то спектр значений энергии частицы дискретен, при отсутствии локализации спектр энергии непрерывен.

Подставим значения k из условия (13.4) в (13.3) и получим

.

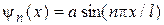Для нахождения константы а воспользуемся условием нормировки, которое в данном случае имеет вид

.

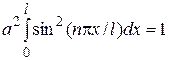На концах промежутка интегрирования подынтегральная функция обращается в нуль. Поэтому значение интеграла можно получить, умножив среднее значение 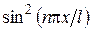(равное, как известно, 1/2) на длину промежутка. Таким образом, получаем 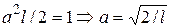. Окончательно собственные волновые функции имеют вид

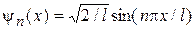(n = 1, 2, 3,...).

Графики собственных значений функций при различных n изображены на рис. 13.2. На этом же рисунке показана плотность вероятности yy^* обнаружения частицы на различных расстояниях от стенок ямы.

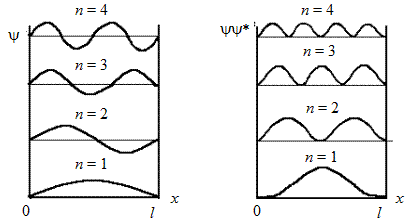
Рис. 13.2

Графики показывают, что в состоянии с n = 2 частица не может быть обнаружена в середине ямы и вместе с тем одинаково часто бывает как в левой, так и в правой половине ямы. Такое поведение частицы, несовместимо с представлением о траектории. Отметим, что, согласно классическим представлениям, все положения частицы в яме равновероятны.

Date: 2015-05-18; view: 1337; Нарушение авторских прав