Гипотеза де-Бройля. Опыт Дэвиссона и Джермера

В результате развития представлений о природе света выяснилось, что в оптических явлениях обнаруживается своеобразный дуализм (двойственность). Наряду с явлениями, которые самым непосредственным образом свидетельствуют о волновой природе света (интерференция, дифракция), имеются и другие явления, столь же непосредственно обнаруживающие его корпускулярную природу (фотоэффект, эффект Комптона).

В 1924 г. французский физик Луи де-Бройль выдвинул гипотезу о том, что дуализм не является особенностью одних только оптических явлений, а имеет универсальный характер. Каждой движущейся микрочастице он поставил в соответствие волновую функцию в виде монохроматической плоской волны. Такая волна характеризуется двумя величинами: частотой w (длиной волны 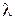) и волновым вектором k. Частоту волны для материальной частицы де-Бройль предложил находить из соотношения Эйнштейна

,

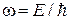где Е – полная энергия частицы. Поскольку импульс фотона равен 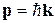, то волновой вектор можно определить соотношением

,

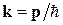где р – импульс материальной частицы. Длина волны де-Бройля 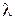, связана с модулем волнового вектора k

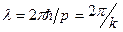. (9.1)

Таким образом, волну де-Бройля можно записать в виде

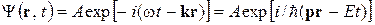, (9.2)

где А – амплитуда; i – мнимая единица; r – радиус-вектор, задающий положение материальной частицы. Функция (9.2) получила название волновой функции, или пси-функции ( 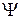-функции). Физический смысл волновой функции в идее де-Бройля оставался неясным.

Гипотеза де-Бройля вскоре была подтверждена экспериментально. Дэвиссон и Джермер в 1927 г. исследовали отражение электронов от монокристалла никеля, имеющего кристаллическую решетку, принадлежащую к кубической системе. Узкий пучок электронов с одинаковой энергией направлялся на поверхность монокристалла, шлифованную перпендикулярно большей диагонали кристаллической ячейки. Отраженные электроны улавливались цилиндрическим электродом, присоединенным к гальванометру. Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. Скорость электронов (или ускоряющее напряжение) и угол j варьировались. На рис. 9.1 показаны результаты эксперимента.

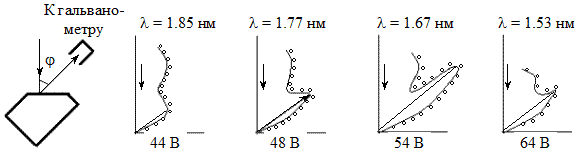
Рис. 9.1

Вертикальная ось на графиках определяет направление падающего луча. Сила тока численно равна длине отрезка, проведенного от начала координат до пересечения с кривой. Рассеяние оказалось особенно интенсивным при определенном значении угла j. Этот угол соответствовал отражению от атомных плоскостей, расстояние между которыми d было известно из рентгенографических исследований. При данном j сила тока оказалась особенно значительной при ускоряющем напряжении, равном 54 В.

Вычисленная по формуле (9.1) длина волны, отвечающая этому напряжению, равна 1,67 нм. Полученные результаты совпадали с расчетами, проведенными по формуле Вульфа – Брэгга

;

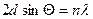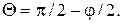
Таким образом, опыт Дэвиссона и Джермера подтверждает гипотезу де‑Бройля. Г. П. Томсон (1927 г.) и независимо от него П. С. Тартаковский получили дифракционную картину при прохождении электронного пучка через металлическую фольгу.

Штерн и сотрудники его лаборатории показали, что дифракционные явления обнаруживаются также у атомных и молекулярных пучков. Во всех перечисленных случаях дифракционная картина соответствует длине волны, определяемой соотношением (9.1). Таким образом, экспериментально было доказано, что все микрочастицы обладают волновыми свойствами.

10. Вероятностный характер волн де-Бройля.
Волновая функция

Микрочастицами называют элементарные частицы (электрон, протон, фотон и др.), а также сложные частицы, образованные из сравнительно небольшого числа элементарных частиц (молекулы, атомы и др.). Своеобразие свойств микрочастиц отчетливо обнаруживается в следующем мысленном эксперименте.

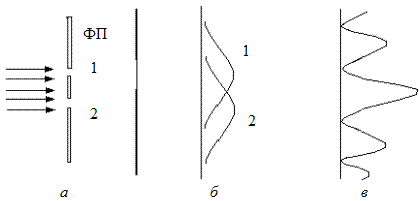
Рис. 10.1

Направим на преграду с двумя узкими щелями параллельный пучок моноэнергетических (т. е. обладающих одинаковой кинетической энергией) электронов (рис. 10.1). Сначала закроем щель 2, получим изображение 1, затем закроем щель 1, получим изображение 2 (рис. 10.1, б). Если оставить оба отверстия открытыми, получаем картину (рис. 10.1, в). Она оказывается аналогичной картине, получающейся при интерференции двух когерентных световых волн. Характер картины свидетельствует о том, что на движение электрона оказывают влияние оба отверстия.

Такой результат несовместим с представлением о траектории. Если бы электрон в каждый момент времени находился в определенной точке пространства и двигался по определенной траектории, он проходил бы через определенное отверстие, первое или второе. Картина, показанная на рис. 10.1, в, указывает на наличие волновых свойств у микрочастиц. Интерференция электронов на двух щелях наблюдалась в эксперименте, проведенном К. Иенссоном в 1961 г.

Немецкий физик Макс Борн предложил рассматривать интенсивность световой волны, или волны де-Бройля, как меру вероятности обнаружения частицы в данном месте пространства.

Пусть dV – некоторый объем в пространстве, в котором находится частица, dP – вероятность нахождения частицы в этом объеме, тогда

,

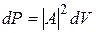где 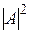является плотностью вероятности обнаружения частицы. Отметим, что в оптике под 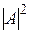обычно понимается интенсивность света.

Движущейся микрочастице ставится в соответствие волновая функция 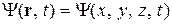, которая представляет собой функцию координат и времени. Вероятность обнаружить частицу в произвольный момент времени t в любой точке с координатами (х, у, z) пропорциональна 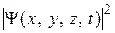. Квадрат модуля используется потому, что 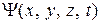– комплексная функция. Формально она обладает свойствами классической волны, поэтому ее называют волновой функцией.

Рассмотрим принцип суперпозиции волновых функций. Если событие может произойти несколькими взаимно исключающими способами (например, двумя), то вероятность этого события представляет собой сумму вероятностей каждого из способов – принцип суперпозиции. В этом случае результирующая волновая функция

.

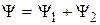Воспользуемся стандартным обозначением: величина со звездочкой обозначает комплексно сопряженную величину. Тогда плотность вероятности равна

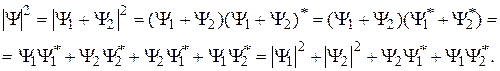
Этот формализм составляет основу волновой и квантовой механики. Приведенное выражение совпадает с правилом сложения амплитуд волн в оптике.

При такой вероятностной интерпретации поведения микрочастиц понятие траектории теряет свой строгий смысл. С помощью Y‑функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.

Вероятностный смысл волновой функции иной, чем в статистической физике. Там предполагается, что частица находится в определенном месте, но из-за большого числа частиц можно составить лишь вероятностное суждение о ее координатах и вычислить вероятность распределения частиц.

В доквантовой физике «понять» означало составить себе наглядный образ объекта или процесса. Квантовую физику нельзя понять в таком смысле слова. Всякая наглядная модель неизбежно будет действовать по классическим законам, и поэтому самое правильное, что можно сделать, это отказаться от попыток строить наглядные модели поведения квантовых объектов. Сочетая в себе свойства частицы и волны, микрочастицы «не ведут себя ни как волны, ни как частицы».

Отличие микрочастицы от привычной для нас макрочастицы заключается в том, что она не обладает одновременно определенными значениями координаты и импульса, вследствие чего понятие траектории применительно к микрочастице утрачивает смысл. Здесь уместно сформулировать общее правило квантовой физики: всякая попытка узнать что-либо о свойствах микрочастиц, всякий эксперимент с ними обязательно меняют их состояние и их волновую функцию.

Ричард Фейман, удостоенный в 1965 г. Нобелевской премии за приложение квантовой механики к электродинамике, писал: «Быть может, вам все еще хочется выяснить: “А почему это? Какой механизм прячется за этим законом?” Так вот: никому никакого механизма отыскать не удалось. Никто в мире не сможет вам “объяснить” ни на капельку больше того, что “объяс­ни­ли” мы. Никто не дает вам никакого более глубокого представления о положении вещей. У нас их нет, нет представлений о более фундаментальной механике, из которой можно вывести эти результаты».

Date: 2015-05-18; view: 1364; Нарушение авторских прав