Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Потенциальная яма конечной глубины
|
|
Рассмотрим задачу о движении частицы в потенциальной яме со стенками конечной высоты 
(рис. 14.1).
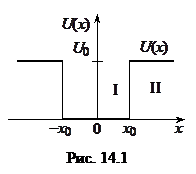Найдем собственные волновые функции 
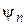и собственные значения энергии 
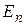, которые удовлетворяли бы граничному условию: при больших значениях 
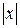функция y(х) стремится к нулю. Рассмотрим только правую половину ямы (
).
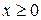В области II уравнение Шредингера записывается в виде
.
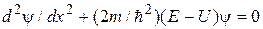Решение этого уравнения имеет вид
,
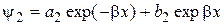где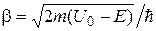 
. При этом в области II 
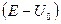< 0. Граничному условию для области II удовлетворяет решение
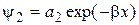. (14.1)
В области I уравнение Шредингера записывается в виде
,
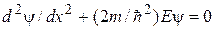а решения этого уравнения имеют вид (см. разд. 13):
● при нечетных значениях n
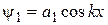; (14.2)
● при четных значениях n
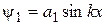, (14.3)
где 
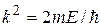2.
При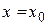 
Y-функция должна удовлетворять стандартным условиям
; 
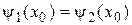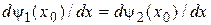. (14.4)
Для нечетных энергетических уровней, подставляя (14.1) и (14.2) в (14.4), получаем соотношения
;
.
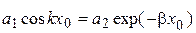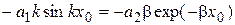Разделив эти соотношения, получим
.
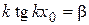Учитывая, что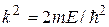 
и 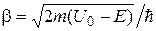, запишем
;
. 
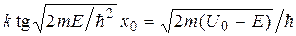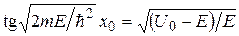. (14.5)
Уравнение (14.5) является трансцендентным и может быть решено либо графически, либо методом итераций, либо методом «проб и ошибок». По найденному любым из этих способов собственному значению энергии 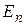(значения положительных корней этого уравнения) можно определить собственные значения Y-функции, и соответственно,
; 
.
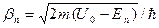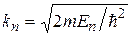Для четных значений n (14.3) запишем граничные условия (14.4) при :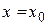
;
.
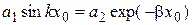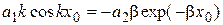Разделив эти соотношения, получим трансцендентное уравнение, которое позволит определить собственные значения энергии и Y-функции на четных энергетических уровнях:
.
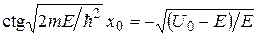Поскольку тангенс и котангенс периодические функции, частица в потенциальной яме может иметь лишь дискретные уровни энергии. Чем глубже яма, тем больше уровней энергии разрешены для частицы, причем уровни, которым отвечают четные и нечетные волновые функции, чередуются.
На рис. 14.2 показаны уровни энергии, а на рис. 14.3 – волновые функции, соответствующие первым трем энергетическим уровням для ямы конечной глубины (сплошные линии) и в бесконечно глубокой потенциальной яме (штриховые линии).
В заключение заметим, что общее решение задачи о частице, находящейся в прямоугольной яме конечной глубины, встречается при рассмотрении многих задач атомной физики, например, эмиссии электронов из металлов, радиоактивного распада и т. д.
Date: 2015-05-18; view: 1353; Нарушение авторских прав