
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Принцип соответствия в квантовой механике
|
|
Критерий, при выполнении которого классическая физика дает достаточную точность и необязательно применять формулы квантовой механики, может быть записан в виде
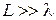 ,
,
где L – размеры системы, в которой движется частица; l – длина волны де‑Бройля.
Смысл его заключается в том, что при длинах волн, много меньших размеров системы, квантово-механические особенности в поведении частиц оказываются несущественными.
Продемонстрируем это утверждение на примере частицы в потенциальной яме (см. разд. 13). Y-функцию частицы (13.5), учитывая, что 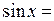
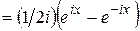 , можно записать в виде
, можно записать в виде
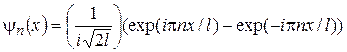 . (15.1)
. (15.1)
Такое представление позволяет говорить о двух движущихся навстречу друг другу волнах де-Бройля. Сравнивая (15.1) с выражением для одномерной волны де-Бройля (9.2), получим выражение для импульса частицы для каждой из этих волн
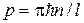
и для длины волны де-Бройля:
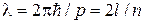 .
.
Очевидно, что при n ® ¥, l ® 0 и поведение частицы должно быть близким к классическому.
Проследим, как это отразится на спектре энергии частицы и ее волновых функциях. Оценим расстояния между соседними уровнями энергии частицы:
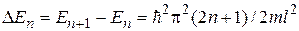 .
.
Относительное расстояние между уровнями
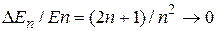 .
.
При n ® ¥ спектр энергии частицы получается почти непрерывным.
Посмотрим теперь, как ведет себя плотность вероятности для частицы при больших n. Для классической частицы плотность вероятности постоянна и равна
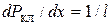 (15.2)
(15.2)
 Плотность вероятности (15.2) постоянна и удовлетворяет условию нормировки
Плотность вероятности (15.2) постоянна и удовлетворяет условию нормировки
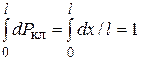 .
.
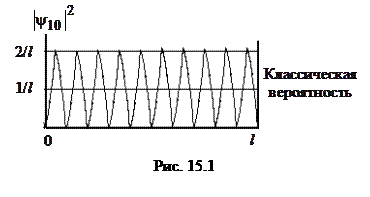
Поведение плотности вероятности при больших n показано на рис. 15.1 (n = 10). Видно, что значение 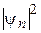 колеблется около среднего значения 1/ l. Физический смысл в этом случае имеет лишь среднее значение плотности вероятности. Поэтому при n >> 1
колеблется около среднего значения 1/ l. Физический смысл в этом случае имеет лишь среднее значение плотности вероятности. Поэтому при n >> 1 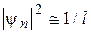 , т. е. квантовая вероятность переходит в классическую.
, т. е. квантовая вероятность переходит в классическую.
Таким образом, по мере возрастания n частица все более утрачивает квантовые свойства, и при больших значениях n квантовая физика переходит в классическую.
Полученный результат является частным случаем общего физического принципа – принципа соответствия: любая новая теория, претендующая на большую общность, чем классическая теория, обязательно должна переходить в старую, классическую теорию в тех случаях, в которых последняя была построена и многократно проверена экспериментально.
16. Прохождение частицы
через потенциальный барьер.
Туннельный эффект
Пусть частица, движущаяся слева направо, встречает на своем пути потенциальный барьер высотой 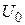 и шириной l (рис. 16.1).
и шириной l (рис. 16.1).
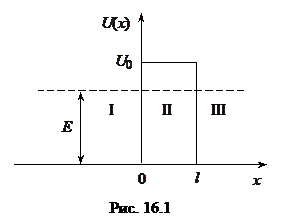 По классическим представлениям, поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера (
По классическим представлениям, поведение частицы имеет следующий характер. Если энергия частицы больше высоты барьера ( ), то частица беспрепятственно проходит над барьером и на участке 0 £ х £ l лишь уменьшается скорость частицы. Затем при х > l скорость принимает первоначальное значение. Если же
), то частица беспрепятственно проходит над барьером и на участке 0 £ х £ l лишь уменьшается скорость частицы. Затем при х > l скорость принимает первоначальное значение. Если же  , то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
, то частица отражается от барьера и летит в обратную сторону; сквозь барьер частица проникнуть не может.
Совершенно иначе выглядит поведение частицы согласно квантово-механическому описанию. Даже при  имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области х > l. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
имеется отличная от нуля вероятность того, что частица проникнет «сквозь» барьер и окажется в области х > l. Такое, совершенно невозможное с классической точки зрения, поведение микрочастицы вытекает непосредственно из уравнения Шредингера.
Рассмотрим случай  [1]. Для областей I и III (U = 0) уравнение Шредингера имеет вид
[1]. Для областей I и III (U = 0) уравнение Шредингера имеет вид
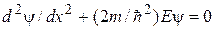 . (16.1)
. (16.1)
Для области II (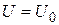 и
и  ) уравнение имеет вид
) уравнение имеет вид
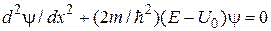 . (16.2)
. (16.2)
Положим, что решение уравнения (16.1) имеет следующий вид:
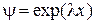 .
.
Тогда подстановка этой функции в уравнение (16.1) приводит к характеристическому уравнению
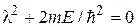 ,
,
где 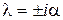 и
и 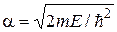 .
.
Общее решение уравнения (16.1) имеет следующий вид:
● для области I:
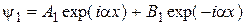 ;
;
● для области III:
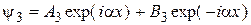 .
.
Решив подстановкой 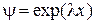 уравнение (16.2), получим общее решение этого уравнения для области II в виде
уравнение (16.2), получим общее решение этого уравнения для области II в виде  , где
, где 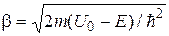 .
.
Заметим, что решение вида 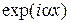 соответствует волне, распространяющейся в положительном направлении оси х, а решение вида
соответствует волне, распространяющейся в положительном направлении оси х, а решение вида 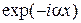 волне, распространяющейся в противоположном направлении.
волне, распространяющейся в противоположном направлении.
В области III имеется только волна, прошедшая через барьер и распространяющаяся слева направо. Поэтому коэффициент 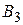 в выражении для
в выражении для 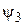 следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся стандартными условиями, которым должна удовлетворять Y‑функция,
следует принять равным нулю. Для нахождения остальных коэффициентов воспользуемся стандартными условиями, которым должна удовлетворять Y‑функция,
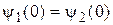 и
и 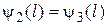 ;
;

 и
и 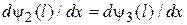 .
.
Из этих условий вытекают соотношения
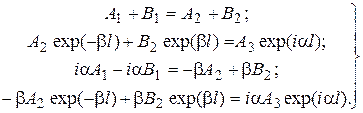 ; (16.3)
; (16.3)
Разделим все уравнения (17.3) на 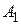 и введем обозначения
и введем обозначения 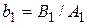 ,
, 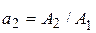 ,
, 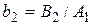 ,
, 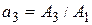 и
и 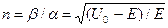 . Тогда уравнения (16.3) примут вид
. Тогда уравнения (16.3) примут вид
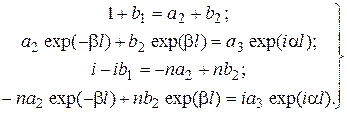 ; (16.4)
; (16.4)
Количественно эффект туннелирования можно оценить, вычислив плотность вероятности 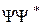 обнаружения частицы в каждой из областей пространства. Оценим степень прозрачности потенциального барьера.
обнаружения частицы в каждой из областей пространства. Оценим степень прозрачности потенциального барьера.
В случае пренебрежения отраженными волнами на границах I – II и II – III, отношение квадратов модулей амплитуд отраженной и падающей волн определяет вероятность отражения частицы от потенциального барьера и может быть названо коэффициентом отражения:
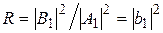 .
.
Отношение квадратов модулей амплитуд прошедшей и падающей волн определяет вероятность прохождения частицы через барьер и может быть названо коэффициентом прохождения (или коэффициентом прозрачности):
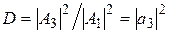 .
.
Коэффициенты отражения и прозрачности связаны соотношением
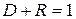 .
.
В результате решения системы уравнений (16.4), получается
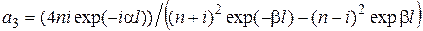 .
.
Значение 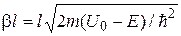 обычно бывает больше единицы, поэтому, учитывая, что
обычно бывает больше единицы, поэтому, учитывая, что 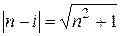 , получим
, получим
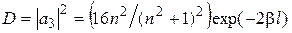 .
.
Отношение 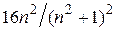 имеет значение порядка единицы. Поэтому окончательно можно считать, что
имеет значение порядка единицы. Поэтому окончательно можно считать, что
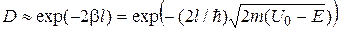 .
.
Из полученного выражения следует, что вероятность прохождения частицы через потенциальный барьер зависит от ширины барьера l и от разности энергий (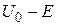 ).
).
Если при какой-либо ширине барьера коэффициент прохождения D равен 0,01, то при увеличении ширины в два раза D станет равным 0,012 = 0,0001, т. е. уменьшится в 100 раз. Тот же эффект вызвало бы возрастание в четыре раза значения (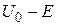 ). Коэффициент прохождения резко уменьшается при увеличении массы частицы m.
). Коэффициент прохождения резко уменьшается при увеличении массы частицы m.
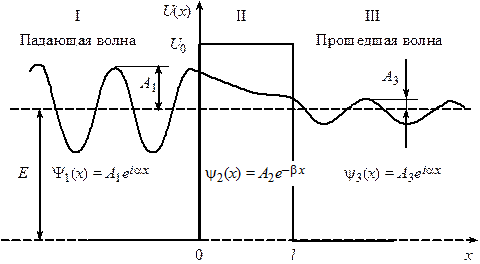
Рис. 16.2
На рис. 16.2 изображены: в области I – действительная часть падающей волны (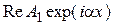 ); в области II – экспоненциально убывающая Y‑функция (
); в области II – экспоненциально убывающая Y‑функция (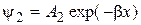 ) и в области III – действительная часть прошедшей волны (
) и в области III – действительная часть прошедшей волны (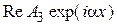 ). Построение выполнено при условии пренебрежения отраженными волнами на границах I – II и II – III, при этом
). Построение выполнено при условии пренебрежения отраженными волнами на границах I – II и II – III, при этом 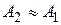 и
и  .
.
В случае потенциального барьера произвольной формы (рис. 16.3) коэффициент прозрачности определяется более общей формулой
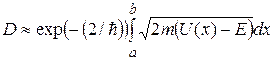 ).
).
 |
При преодолении потенциального барьера частица как бы проходит через «туннель» в этом барьере, в связи с чем рассмотренное нами явление называют туннельным эффектом. На основе этого эффекта построены многие современные приборы, например туннельные диоды и транзисторы.
Рассмотрим случай, когда 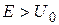 (рис. 16.4). Для области I уравнение Шредингера имеет вид
(рис. 16.4). Для области I уравнение Шредингера имеет вид
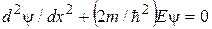 , (16.5)
, (16.5)
для области II
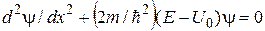 . (16.6)
. (16.6)
Общие решения уравнений (16.5) и (16.6) имеют следующий вид:
● для области I
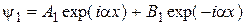 ;
;
● для области II
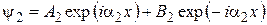 ,
,
где 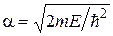 и
и 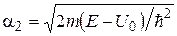 .
.
Заметим, что, как и в случае высокого потенциального барьера, решение вида 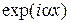 соответствует волне, распространяющейся в положительном направлении оси х, а решение вида
соответствует волне, распространяющейся в положительном направлении оси х, а решение вида 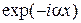 – волне, распространяющейся в противоположном направлении.
– волне, распространяющейся в противоположном направлении.
В области II имеется только волна, прошедшая над барьером и распространяющаяся слева направо. Поэтому коэффициент 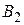 в выражении для
в выражении для 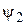 следует принять равным нулю. Для нахождения остальных коэффициентов можно воспользоваться стандартными условиями, которым должна удовлетворять функция
следует принять равным нулю. Для нахождения остальных коэффициентов можно воспользоваться стандартными условиями, которым должна удовлетворять функция 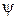 :
:
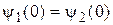 ;
;  . (16.7)
. (16.7)
В области II 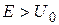 , следовательно, действительная часть волновой функции
, следовательно, действительная часть волновой функции 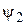 (
(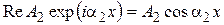 ) представляет собой косинусоиду с волновым числом
) представляет собой косинусоиду с волновым числом
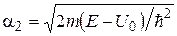 .
.
При 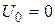 длина волны (волновое число
длина волны (волновое число 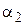 ) действительной части Y‑функции в области II совпадает с длиной волны действительной части волновой функции в области I. С ростом
) действительной части Y‑функции в области II совпадает с длиной волны действительной части волновой функции в области I. С ростом 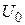 значение волнового числа
значение волнового числа 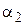 уменьшается (длина волны увеличивается), и в пределе при
уменьшается (длина волны увеличивается), и в пределе при 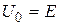 действительная часть волновой функции в области II перестает быть гармонической. На рис. 16.5 изображены действительная часть падающей волны (
действительная часть волновой функции в области II перестает быть гармонической. На рис. 16.5 изображены действительная часть падающей волны (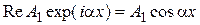 ) и действительная часть прошедшей волны (
) и действительная часть прошедшей волны ( ).
).
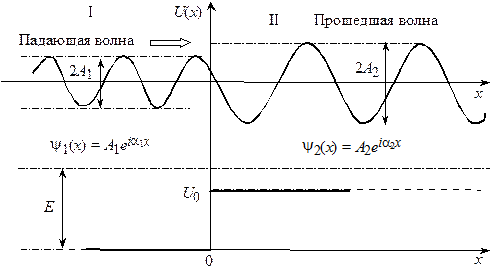
Рис. 16.5
Используя стандартные условия (16.7), можно показать, что коэффициент отражения 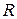 и коэффициент прохождения
и коэффициент прохождения 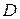 для низкого (
для низкого (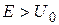 ) потенциального барьера бесконечной ширины имеют вид
) потенциального барьера бесконечной ширины имеют вид
 ;
; 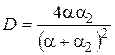 .
.
Date: 2015-05-18; view: 978; Нарушение авторских прав