Связь КЭХ с квантованием проводимости в нитях

Формула (7.2), предсказывающая квантование проводимости в

баллистических квантовых нитях, совершенно неожиданно имеет

такой же вид, как и формула (6.9) из теории КЭХ. Оказывается,

такое совпадение не случайно. Несмотря на то что в отсутствие

магнитного поля одномерные системы, какими являются

квантовые нити, принципиально отличаются от двумерных электронных

систем, последние в сильном магнитном поле приобретают черты,

свойственные квантовым нитям.

Чтобы понять, в чем здесь дело, надо рассмотреть общие черты

динамики двумерных электронов в магнитном поле Н,

перпендикулярном их плоскости. Как отмечалось в разделе 6.1, электроны в

Н движутся по круговым орбитам с частотой 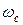, что с точки

зрения квантовой механики отвечает энергетическому спектру в виде

эквидистантных уровней Ландау. Это, однако, относится лишь к

электронам в центральной части образца, вдали от его границ.

Совсем иначе ведут себя электроны, находящиеся вблизи границы

образца. Как видно из рис. 7.2, за счет многократных отражений от

границы они получают возможность поступательного движения

вдоль края. Это движение может быть охарактеризовано некоторым

средним значением импульса 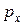, параллельного границе, и со-

соответствующей кинетической энергией Е. Таким образом, динамика приграничных двумерных электронов в сильном магнитном поле

напоминает их динамику в квантовых нитях, где электроны

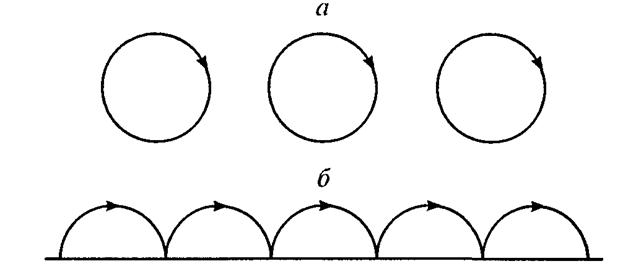
Рис. 7.2. Траектории двумерных электронов в перпендикулярном

магнитном поле в глубине образца (а) и вблизи границы {б).

могут двигаться в одном направлении и резко ограничены в своем

движении в двух других.

И еще одно важное замечание. В квантовой нити без магнитного

поля ток, параллельный оси нити, создается электрическим полем,

имеющим то же самое направление. В магнитном поле сила,

действующая на электрон со стороны электрического поля (сила

Лоренца), перпендикулярна как электрическому, так и магнитному

полю. Поэтому формула типа (7.2) в магнитном поле будет связывать

между собой x-компоненту электрического поля с y-компонентой

тока, и наоборот. Итак, мы можем окончательно утверждать, что в

двумерном электронном газе в сильном магнитном поле недиагональная холловская компонента проводимости дается выражением

(7.2), что составляет основное содержание КЭХ и может рассматриваться

как его альтернативный качественный вывод, использующий иную физическую модель, нежели в главе 6.

Важным отличием КЭХ от проводимости квантовой нити является

тот факт, что вдоль данной границы электроны могут двигаться лишь

в одну сторону. Движение в другую сторону осуществляется вдоль противоположной границы образца. При этом становится

невозможным упругое отражение электронов, т. е. смена знака

импульса за счет упругого рассеяния на примесях или дефектах.

Такой процесс требовал бы перескока электрона на макроскопическое расстояние от одной границы до другой, что невозможно при

рассеянии. Поэтому в отличие от нитей, где рассеяние носителей

назад способно привести к значительным отклонениям проводимости

от универсального значения (7.2) (см. формулу (7.3)), в

условиях КЭХ данный результат является точным.

Date: 2015-05-18; view: 687; Нарушение авторских прав