Баллистическая проводимость нитей

Характер проводимости квантовых нитей существенно зависит

от их длины. Если длина нити L существенно превосходит длину

свободного пробега носителей l, то удельная проводимость нити

в расчете на единицу длины дается обычным классическим выра-

выражением, 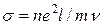где 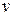— тепловая скорость носителей.

Различие с массивным образцом будет лишь в том, что рассеяние

носителей в нити и в массивном образце может быть весьма

разным, в связи с чем длина пробега 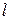в нити дается совсем иными

выражениями и требует специального анализа для своего

нахождения.

Значительно более интересна и необычна ситуация L < .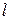

При этом электрон, вылетев из одного контакта, долетает до

другого контакта без столкновений, как снаряд, выпущенный из

пушки. Такая аналогия привела к тому, что рассматриваемые

бесстолкновительные структуры часто называют баллистическими.

Пусть имеется баллистическая одномерная структура, снабженная металлическими контактами, между которыми мы приложили

напряжение V. Контакты можно рассматривать как электронные

резервуары, характеризуемые химическими потенциалам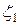и и ,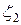

причем 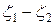= eV. Для простоты будем считать температуру

достаточно низкой, так что электроны в резервуарах полностью

вырождены. В области энергий 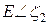состояния в левом и правом

контактах полностью заполнены, так что электроны из этих

состояний не могут создавать ток в цепи. Такой ток связан исключительно

с электронами из энергетического интервала 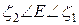где в

левом контакте есть электроны, вылетающие в нить, а состояния

правого контакта пусты и способны эти электроны принять.

Вычислим величину возникающего тока.

Если электрон имеет импульс 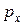и, следовательно, скорость

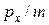, то его вклад в ток равен 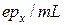. Для получения полного тока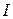

нам необходимо сложить такие вклады от всех электронов с энер-

энергиями 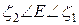во всех подзонах:

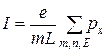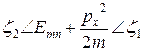, . (7.1)

Если разность 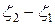мала, то интересующие нас электроны

существуют только в подзонах с 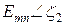, причем импульсы их лежат

в интервале длиной 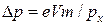вблизи 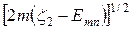. Из

сказанного ранее следует, что в интервале 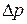с учетом спинового

вырождения есть 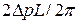различных электронных состояний, и

окончательно из (7.1) имеем , где N — число уровней

(подзон), лежащих ниже уровня химического потенциала, т. е.

содержащих электроны.

Итак, наши выкладки привели к тому, что проводимость балли-

баллистической квантовой нити

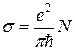. (7.2)

Полученная формула носит общий характер и не зависит ни от ха-

характеристик нити (за исключением числа заполненных уровней),

ни от условий измерений. Как и формула для КЭХ (6.9), она не

содержит ничего, кроме мировых констант.

Необходимо обратить внимание еще на один важный вопрос.

Наличие конечной проводимости у системы означает, что при

приложении к ней напряжения V в системе протекает ток и происхо-

происходит выделение энергии, равное 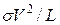, в единицу времени. Это

аналог эффекта Джоуля—Ленца в обычном проводнике. Физика джоу-

левых потерь хорошо известна: электроны, разгоняющиеся в

электрическом поле, отдают энергию кристаллической решетке за счет

столкновений. Но в баллистической нити электроны не испытывают столкновений! Откуда же берутся тепловые потери? Они происходят

не в самой нити, а в контактах, причем в обоих контактах

поровну. Известно, что в системе вырожденных электронов весь

токоперенос осуществляется электронами на уровне Ферми.

Иными словами, все электроны, поступающие в левый контакт из

внешней цепи, имеют энергию 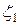. Уходят же из контакта в нить

электроны из интервала энергий 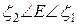, т.е. со средней

энергией 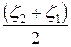. Таким образом, если мы считаем, что распределение электронов в левом контакте равновесно и не меняется со временем, то каждый электрон, приходящий из внешней цепи, должен за счет рассеяния в контакте отдать кристаллической решетке энергию, в среднем равную 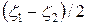. Аналогичная ситуация и в правом контакте. В него из нити поступают электроны с энергиями от 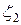до 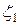Приходя в равновесие, они должны «остыть» до значения С,2 и тем самым отдать энергию, также в среднем равную .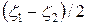

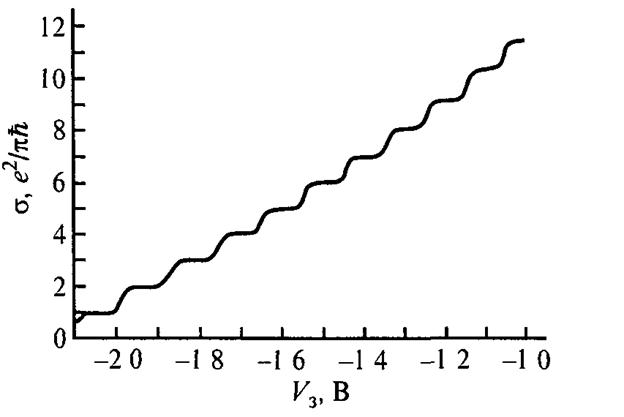
Рис 7.1. Экспериментальная зависимость проводимости квантовой нити

(точечного контакта) от напряжения на затворе, определяющего концент-

концентрацию носителей.

Интересно проследить, как зависит проводимость баллистической

нити от концентрации электронов в ней. В структурах с затвором

Шоттки концентрацию можно менять с помощью напряжения, прикладываемого к затвору. По мере уменьшения отрицательного потенциала на затворе ширина квантовой нити и концентрация носителей

в ней возрастают. При этом возрастет число заполненных квантово-размерных подзон, как за счет роста концентрации, т. е. уровня Ферми,

так и за счет уменьшения энергетического расстояния между квантовыми уровнями. Если температура низка и электроны в структуре полностью вырождены, то каждый раз, когда очередной уровень 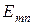пересекает уровень Ферми, число N в формуле (7.2) меняется на единицу и проводимость нити возрастает на 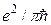. В целом зависимость от напряжения на затворе будет иметь вид ступенчатой функции, показанной на рис. 7.1.

Если нить не является достаточно короткой и высококачественной,

то электрон на пути от контакта до контакта может испытать рассеяние на примеси или ином дефекте нити. Такое рассеяние является упругим, т. е. происходит без изменения энергии. Если электрон остается на том же квантовом уровне 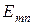, то упругое рассеяние можно осуществить лишь одним образом: сменив импульс 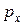на - 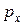, т. е. повернув строго назад (в двух и трехмерном случаях возможности для упругого рассеяния значительно больше: вектор импульса, не меняясь по величине, может повернуться на любой угол по отношению к своему начальному направлению). Естественно, что ток при этом уменьшается. Если для электрона из подзоны mn вероятность такого отражения равна 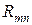, то вместо формулы (7.2) мы будем иметь:

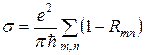. (7.3)

За счет зависимости коэффициентов отражения 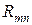от энергии

электронов, а также за счет теплового размытия функции

распределения носителей ступеньки, даваемые формулой (7.3), могут

быть несколько размыты, однако в реальных высококачественных

структурах они могут наблюдаться очень отчетливо.

Экспериментальные исследования описанного квантования

проводимости в коротких (баллистических) нитях часто проводятся

на структурах, представляющих собой, строго говоря, не нить как

таковую, а так называемый точечный контакт, т. е. узкую перемычку, соединяющую собой два участка двумерного электронного газа

достаточно большой площади. Формально это как бы нить,

имеющая длину, сравнимую с ее шириной, причем последняя имеет

достаточно малую величину. Квантование проводимости должно

наблюдаться и в таких структурах (это неудивительно, поскольку

окончательная формула (7.2) не содержит никаких конкретных

параметров, описывающих размеры и форму нити). В частности,

экспериментальные зависимости, показанные на рис. 7.1, получены

именно на таком квантовом микроконтакте.

Date: 2015-05-18; view: 1345; Нарушение авторских прав