Соотношение неопределенностей. Волновой дуализм

При описании состояния движения классической частицы пользуются заданием обобщенных координат и обобщенных импульсов: .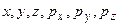

Как описывать состояние движения микрочастицы?

Микрочастица обладает корпускулярно-волновой природой, но это не означает, что при задании состояния движения ей следует приписать все свойства частиц и все свойства волн. То, что это не классическая частица означает: описание корпускулярных свойств вряд ли можно проводить с помощью канонических переменных, одновременно задавая координаты и сопряженные им импульсы.

Действительно, микрочастице, движущейся с импульсом 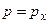, сопоставляется плоская монохроматическая волна де Бройля с длиной 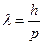. Но отсюда следует: для такой частицы нельзя одновременно точно задавать и 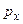, так как задание 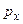означает задание длины волны , что в свою очередь предполагает задание некоторой области пространства. Другими словами, выражение "длина волны микрочастицы, имеющей координату , лишено смысла.

Таким образом, в квантовой области нет таких микрообъектов, у которых координата и сопряженный ей импульс одновременно имеют точные (определенные) значения. Если же все-таки и координату , и соответствующую проекцию импульса 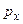указывать (измерять) одновременно, то обязательно возникнут неопределенност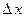и и 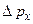, причем произведение этих неопределенностей по порядку величины не меньше постоянной Планка:

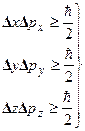, (2.10)

Это знаменитые соотношения неопределенности Гейзенберга выражают корпускулярно-волновую природу микрообъекта.

Рассмотрим свободно движущуюся частицу и импульсом 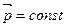(). При точно заданном импульсе неопределенности 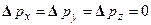, тогда из соотношений (2.10) следует, что бесконечно велики, т.е. координаты частицы совершенно не определены, это означает, что частицу с равной вероятностью можно обнаружить в любой точке пространства. При этом величина квадрата модуля волны де Бройля, сопоставляемой свободно движущейся частице с импульсом 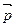, оказывается постоянной:

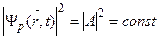. (2.11)

Свободно движущаяся частица с заданным импульсом является идеализацией. Какая же волна описывает волновые свойства у частицы, локализованной в некоторой области пространства, например, 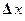? Интересующую нас волну, связанную с областью локализации 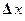, можно получить как суперпозицию плоских монохроматических волн де Бройля с импульсом, изменяющимся непрерывно в интервале от 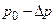до :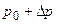

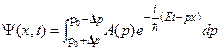. (2.12)

Такая группа волн называется волновым пакетом.

Для исследования вида функции (2.12) вычислим приближенно интеграл в этой формуле. Если интервал 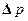достаточно мал, то можно считать

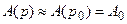, (2.13)

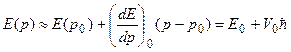, (2.14)

где

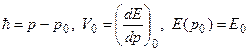. (2.15)

Подставляя выражения (2.13), (2.14), (2.15) в соотношение (2.12), получаем

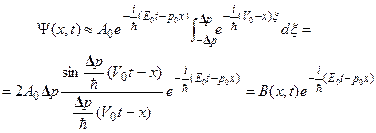. (2.16)

Квадрат модуля этой волны, равной квадрату модуля ее амплитуды, представляется формулой:

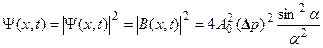, (2.17)

где

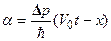. (2.18)

График функции 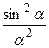, с точностью до постоянного множителя, представляющий график 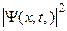, дан на рис.1.5.

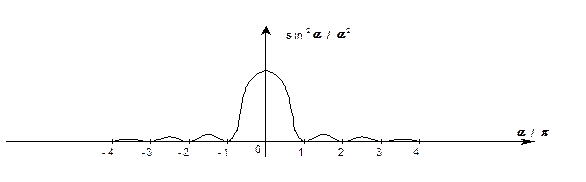
Рис. 1.5.

Эта функция заметно отлична от нуля лишь в интервале от -p до p. Вне указанного интервала значения функции 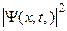могут быть приравнены нулю. Поэтому частица с подавляющей вероятностью находится на участке оси 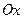между точкам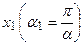и и 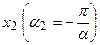. Длина участка 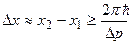, отсюда следует одно из соотношений неопределенностей:

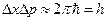. (2.19)

Следует заметить, что групповая скорость (скорость центра волнового пакета) равна скорости движения частицы 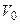. Если учесть высшие члены в разложении (2.14), то окажется, что с течением времени волновой пакет расплывается, захватывая все большую область пространства. В связи с этим нельзя волной пакет связать со структурой частицы, т.е. волновая функция описывает состояние частицы и позволяет судить о вероятности ее обнаружения в различных точках пространства.

Date: 2015-05-18; view: 460; Нарушение авторских прав