Гипотеза де Бройля. Волна де Бройля

Французский физик Луи де Бройль, анализируя идею дуализма и уравнения Эйнштейна, выдвинул в 1924 году гипотезу о возможности их обобщения на микрообъектах и в первую очередь на электронах. Эта гипотеза была им высказана с целью физического обоснования квантования энергии электронов в атоме (теория Бора) и для объяснения первых опытов по дифракции электронов.

Высказав гипотезу о том, что корпускулярно-волновой дуализм свойственен не только свету, но и материальным телам, де Бройль предложил с каждым микрообъектом связывать корпускулярные характеристики (энергию 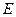и импульс 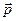) и волновые характеристики (частоту 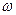и волновой вектор 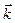). Взаимосвязь между ними должна быть релятивистки ковариантной, т. е. записана в четырехмерной форме. Используя четырехмерную запись вектора импульса и волнового вектора в виде:

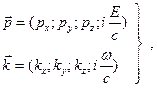(2.6)

де Бройль записал соотношение между ними с помощью постоянной Планка

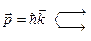
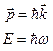. (2.7)

Таким образом, уравнения Эйнштейна (2.7), благодаря гипотезе де Бройля, приобрели универсальный характер и стали одинаково применимы как для анализа корпускулярных свойств света, так и при исследовании волновых свойств движущихся микрообъектов (объектов).

Из уравнения (2.7) следует:

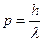, (2.8)

т.е. микрочастице с импульсом 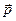сопоставляется плоская монохроматическая волна с длиной . Эта волна называется волной де Бройля, определяется формулой:

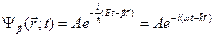(2.9)

Вскоре гипотеза де Бройля получила надежное экспериментальное обоснование. В 1923 году Дэвиссон и Кунсман, наблюдая рассеяние пучка электронов от поверхности кристалла, обнаружили дифракционные максимумы. В 1927 году Дэвиссон и Джермер подтвердили этот результат в специально поставленных опытах по обнаружению волновых свойств электронов (рассеяние электронов на монокристаллах Ni). В экспериментах Тартаковского и Томсона были обнаружены дифракционные кольца, образованные электронами, прошедшими через фольгу из поликристаллического вещества. В этих исследованиях по результатам измерения радиусов 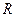дифракционных колец, вычислялась длина волны де Бройля; импульс электронов был заранее известен (электроны ускорялись в электронной пушке). В результате формула (2.8) получила блестящее подтверждение.

Позднее наблюдалась дифракционная картина от атомов, молекул, нейтронов и других частиц. В 1947 году советские физики Сушкин, Фабрикант и Биберман поставили интересный опыт, пропуская через дифракционное устройство электроны из пучка один за другим; на экране при этом вновь наблюдалась дифракционная картина. Тем самым экспериментально было доказано: волновые свойства присущи не коллективу электронов в пучке, а каждому электрону.

Итак, микрообъект есть специфический объект, способный в зависимости от условий проявлять в той или иной мере корпускулярные и волновые свойства, т.е. корпускулярно-волновой дуализм следует понимать, как потенциальную способность микрообъекта проявлять в различных внешних условиях различные свойства.

Date: 2015-05-18; view: 565; Нарушение авторских прав