Геометрические символы

Геометрию обычно рассматривают как науку, в которой мы обнаруживаем и изучаем законы пространства. В более общем смысле ее можно рассматривать как науку о представлении, без каких-либо ограничений только пространство-подобными отношениями. Например, сейчас привычно говорить о четырехмерной геометрии пространства-времени и даже об N-мерной геометрии неспециализированного характера. Мы, следовательно, можем принять термин геометрия для того, чтобы обозначить изучение представления.

Язык математики требует применения чисел, и возникает вопрос, какая степень независимости между различными наборами чисел необходима, чтобы дать адекватное представление о событии. Независимый набор чисел называется измерением /dimension/, а некоторое множество таких наборов мы называем многообразием /manifold/. Одной из задач наук о системах координат является определение наиболее подходящего многообразия для представления всех гипономных сущностей. Каждое целое является – в отношении своей простой целостности – единицей, неотличимой от любой другой единицы, и, следовательно, может быть представлено числом одни. Однако, поскольку оно познаваемо и в других отношения, потребуется массив чисел для представления различных ситуаций, в которые оно может входить.

В соответствии с последовательностью категорий представление должно начинаться с целостности. Мы воспользуемся термином " точка " для обозначения целого безотносительно к бытию или функции. Первичный жест – акт представления – есть жест указания и "выделения точки"[3], который равносилен фиксации одного целого А как отличного от всех других целых не-А. Жест, фиксирующий точку как целое, закончен в себе. Он игнорирует все, кроме обозначаемой точки и, следовательно, не достигает категории полярности. Следовательно, точка не имеет ни силы, ни величины. Каждое целое, понимаемое только как целое, может быть представлено точкой.

Категория полярности может быть эксплицирована, только когда есть две независимые точки. Мы будем использовать термин " интервал " для обозначения этого уникального свойства, которое определяется двумя точками А и В безотносительно к какому-либо другому целому. Ввиду этого последнего условия интервал не имеет направления. В геометрии трехмерного пространства интервал – это длина и ничего более. Во временном измерении это не что иное как продолжительность. Детерминирующие условия вечности и гипарксиса также должны иметь свои интервалы, и там, где это должно быть специфицировано, мы пользуемся терминами "апокритический интервал" и "гипархческий интервал". Жест, обозначающий интервал, является жестом разделения и, следовательно, предполагает силу. Интервал между двумя геометрическими точками не содержит силу в физическом смысле и, тем не менее, он передает понятие полярности. Однако, это просто полярность без соотнесенности. Для обозначения интервала между двумя точками А и В, независимо от их природы, мы будем использовать символ /АВ/. Слово "интервал" берется в одном и том же смысле, имеет ли оно отношение к длинам или продолжительностям, которые мы можем измерять, или к апокризису и гипарксису, ускользающим от нашего наблюдения.

Чтобы обозначить отношение, мы вводим третий символ, а именно – вектор. Вектор не может быть определен в терминах только интервала; он имеет направление и величину, и они могут быть установлены только посредством отнесения, независимого от точек А и В, которыми задается векторный интервал. Жест, связывающий А и В, не имеет значения, если он не включает разделяющую их силу. Вектор, следовательно, - это представление акта преодоления сопротивления. Переход от А к В связывает А с В и В с А, но делает это таким образом, что различает эти два направления. Когда предполагается, А и В – это известные сущности, мы представляем соединяющий их вектор символом 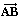. Когда мы хотим обозначить векторный жест без ссылки на две особые сущности, мы используем символ V. Несколько различных векторов обозначаются символами того же вида V, W, U и т.д.

Предположим, что для представления любой возможной оказии требуются N независимых числовых множеств. Тогда точка определяется как комбинация N чисел, взятых по одному из каждого множества.[4]

Необходимо также определить четвертый символ [N] – N-мерное многообразие – обозначающий многообразие, каждая точка которого единственным образом определена при помощи независимых чисел. Отдельная точка – это [0], линия - [1], поверхность - [2], и т.д. Говорят, что [N] имеет N измерений. Любые две точки А и В из [N] единственным образом определяют интервал, представляемый символом /АВ/. Могут существовать также векторы 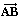, имеющие как величину, так и направление, но не обязательно уникальные, так как качества, переносимые от А к В, могут различаться. Векторы сами по себе не могут служить для представления таких многомерных переходов; но, как будет показано позже, может быть построена такая геометрия, в которой могут быть определены семейства векторов с необходимыми свойствами. Они будут называться пучками, и их применение к физическим проблемам является одним из принципиально новых математических методов, принимаемых в данной работе.

В дополнение к этим пяти первичным символам необходимые операции могут представляться при помощи обычных математических символов суммирования, дифференцирования и комбинации матриц и тензоров. Другим понятиям, таким как тождественность, конгруэнтность, равенство и неравенство могут быть присвоены их обычные значения, хотя, как это обнаружится позднее, некоторые из них окажутся подверженными относительности значения, сопровождающей все утверждения о бытии и существовании.

Date: 2015-05-18; view: 555; Нарушение авторских прав