Задача № 42

Определите возможные результаты измерений проекции момента импульса 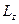на выделенное направление для частицы, находящейся в состоянии, описываемом волновой функцией 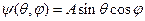, где 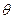- полярный угол, 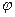- азимутальный угол, 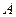- некоторая нормировочная постоянная.

Решение:

Если некоторая физическая величина имеет точно определённые значения в некотором состоянии, то такое состояние называется собственным. Пси-функции собственных состояний являются решением операторного уравнения:

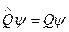(1)

где 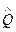- оператор физической величины 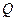, в правой части 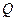- собственное значение этой физической величины. В нашей задаче необходимо определить собственные значения проекции момента импульса 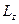, поэтому операторное уравнение (1) в нашем случае имеет вид:

(2)

где 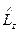- оператор проекции момента импульса на ось z, который в сферических координатах имеет вид:

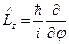(3)

Найдём собственные пси-функции, соответствующие состояниям, в которых проекция момента импульса на ось имеет определённые значения. Для этого решим операторное уравнение:

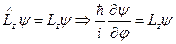(4)

Решая дифференциальное уравнение (4), получим:

(5)

где 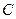- постоянная, которую найдём из условия нормировки:

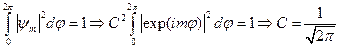(6)

В этом случае собственные пси-функции имеют вид:

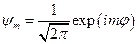(7)

Определим постоянную 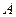в выражении для пси-функции данного состояния, используя условие нормировки:

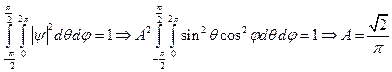(8)

Тогда пси-функция данного состояния имеет вид:

(9)

Разложим эту пси-функцию в ряд по собственным пси-функциям (7), учитывая, что :

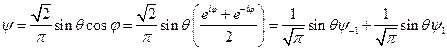(10)

Пси-функция (9) раскладывается по двум собственным пси-функциям, имеющим квантовые числа . Соответственно, проекция момента импульса на произвольную ось z в состоянии, описываемом пси-функцией (9), принимает значения:

(11)

Ответ:

.

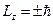Date: 2015-05-18; view: 742; Нарушение авторских прав