
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм
|
|
Задача 15. Исследование спектра излучения Солнца показало, что максимум спектральной плотности энергетической светимости соответствует длине волны 0,5 мкм. Определить энергетическую освещенность поверхности Земли, принимая Солнце за абсолютно черное тело.
| Дано: lmax = 0,5 мкм = 5 × 10–7 м r c = 6,96 × 108 м r = 1,5 × 1011 м s = 5,67×10–8 Вт/(м2×К4) | Решение Энергетическая освещенность поверхности Земли равна потоку солнечной энергии, падающей на единицу поверхности Земли. Будем считать Солнце сферой, площадь поверхности которой |
| Е э –? | S = 4 p r c2. |
Поток энергии, излучаемой Солнцем,
Ф с = R э × 4 p R 2,
где R э = s . T 4c, так как, по условию задачи, Солнце – абсолютно черное тело.
Ф с = s . T 4c × 4 p R 2.
Температуру поверхности Солнца Т с определим из закона Вина
Т с = b ΄ / l max .
Поток солнечной энергии распространяется от Солнца по всем направлениям в пределах 4p радиан (в дальнейшем будем считать Солнце точечным источником). На единицу любой поверхности находящейся на расстоянии r от Солнца, приходится энергия, равная Ф с / (4p . r 2).
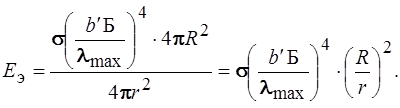
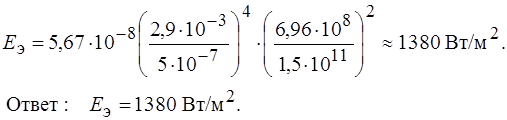
Задача 16. Внутри солнечной системы на том же расстоянии от Солнца, как и Земля, находится частица сферической формы. Полагая Солнце абсолютно черным телом с температурой Т с = 6000 К и что температура частицы во всех ее точках одинакова, определить ее температуру, считая частицу серым телом.
| Дано: r = 1,5.1011 м Т с = 6000 К R с = 6,96.108 м l= 500 нм | Решение Частица – серое тело, следовательно, ее поглощательная способность одинакова для всех длин волн и при данной температуре частиц а l, Т = аT . Так как температура частицы постоянна во всех ее точках, соблюдается условие равновесия: |
| Т r –? | мощность излучения, поглощаемого частицей, равна |
мощности излучения, испускаемой ею
N погл = N изл.
Определим N погл, исходя из объяснения решения предыдущей задачи. Мощность солнечного излучения, падающего на единицу поверхности частицы, равна
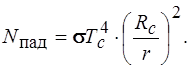
Если учесть, что к Солнцу обращена половина поверхности частицы, то на поверхность частицы падает мощность солнечного излучения, равная
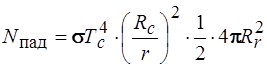 ,
,
где R c – радиус частицы.
Частица – это серое тело, поэтому она поглощает не всю энергию, а только часть ее.
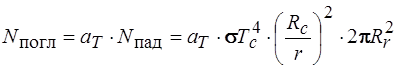 .
.
Определим энергию, излучаемую частицей
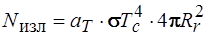 .
.
Приравнивая правые части последних соотношений, получим
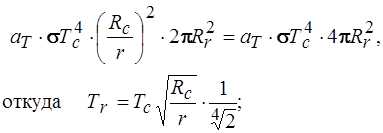
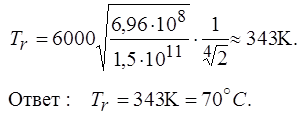
Задача 17. Определить, за какое время зачерненный металлический шар диаметром D остынет с температуры T 1 до температуры T 2. Теплоемкость шара С. Остывание идет только за счет теплового излучения.
Решение
Теплоемкость твердого тела определяется формулой
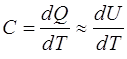 ,
,
где dU – это изменение внутренней энергии, так как при нагревании происходит незначительное изменение объема тела.
Вследствие теплового излучения происходит убыль внутренней энергии шара, равная d U = – C d T.
С другой стороны, энергия, излучаемая нагретым шаром за время dt, равна dE = s T 4 × 4p R 2 × d t.
Приравнивая правые части последних соотношений, получим
– C d T = s T 4 × 4p R 2 × d t.
Проводим разделение переменных и решаем полученные интегралы

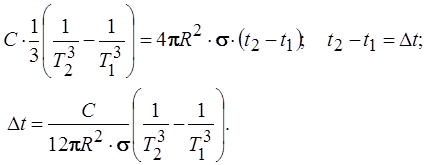
Date: 2015-05-18; view: 3807; Нарушение авторских прав