
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Дифракция света. Дифракция на одной щели
|
|
Основные формулы:
Дифракция на одной щели.
При нормальном падении лучей на щель шириной a
условие дифракционных максимумов
a sin j = (2 k +1) l/2, (k =1, 2, 3...)
условие дифракционных минимумов
a sin j = k l, (k =1, 2, 3...)
Дифракция на плоской дифракционной решетке.
При нормальном падении лучей на решетку с периодом d
условие главных дифракционных максимумов
d sin j = k l, (k =1, 2, 3...)
условие добавочных минимумов
d sin j = k l/ N,
где N – число щелей (штрихов решетки), k = 1, 2, 3..., кроме значений k = N, 2 N, 3 N...
Разрешающая способность дифракционной решетки
R = l/(d l) = kN,
где dl – наименьшая разность длин волн двух соседних спектральных линий (l и l +d l), при которой эти линии могут быть видны раздельно.
Угловая дисперсия дифракционной решетки
D j = d j / d l = k / (d × cos j).
Линейная дисперсия дифракционной решетки D l = 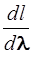 .
.
Для малых углов дифракции D l» F × D j,
где F – фокусное расстояние линзы, собирающей на экране дифракционную картину.
Примеры решения задач
Задача 6. На пути луча, идущего в воздухе, поставили диафрагму с круглым отверстием, пропускающим: 1) половину первой зоны Френеля; 2) первую зону Френеля; 3) первые полторы зоны Френеля. Как изменилась при этом интенсивность света в точке наблюдения, находящейся на оси отверстия?
Решение

| 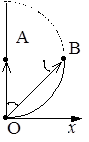
| 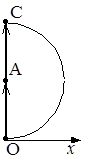
| 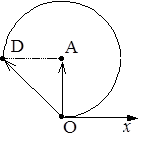
|
| а | б | в | г |
| Рис. 6 |
1) Задачу решаем методом графического сложения амплитуд. В случае, когда идет луч в воздухе, векторная диаграмма имеет вид, представленный на рис. 6, а. Вектор, соединяющий начало диаграммы (т. О) с конусом (т. А), является вектором амплитуды колебания, возбуждаемого в точке наблюдения всей волновой поверхностью.
На рис.6,б представлена векторная диаграмма, соответствующая случаю, когда отверстие пропускает половину первой зоны Френеля. Световой эффект в этом случае определяется вектором 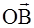 .
.
Из рис. 6 видно, что ОВ = ОА / (cos45 ˚) = OA× 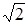 . Интенсивность световой волны пропорциональна квадрату ее амплитуды J ~A 2, следовательно, интенсивность света в первом случае (рис. 6, а) J 1 ~ОA 2, во втором случае (рис. 6, б) J 2 ~ОВ 2.
. Интенсивность световой волны пропорциональна квадрату ее амплитуды J ~A 2, следовательно, интенсивность света в первом случае (рис. 6, а) J 1 ~ОA 2, во втором случае (рис. 6, б) J 2 ~ОВ 2.
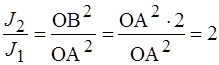 , следовательно, интенсивности увеличиваются в два раза.
, следовательно, интенсивности увеличиваются в два раза.
2) Во второй задаче отверстие пропускает первую зону Френеля. Векторная диаграмма для этого случая представлена на рис. 6, в. Результирующая амплитуда – вектор ОС. Из рис. 6, в видно, что ОС=2 · ОА, следовательно, 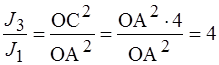 , то есть интенсивность увеличивается в 4 раза.
, то есть интенсивность увеличивается в 4 раза.
3) Векторная диаграмма для решения третьей задачи представлена на рис. 6, г. Результирующий вектор амплитуды – вектор ОD. Сравнение рис. 6, б и 6, г показывает, что ОD = ОВ, следовательно, ответ будет такой же, как на первый вопрос задачи.
Ответ: 1) увеличивается в 2 раза;
2) увеличивается в 4 раза;
3) увеличивается в 2 раза.
Задача 7. На диафрагму с диаметром отверстия 1,96 мм рис. 7 падает нормально параллельный пучок монохроматического света (l=600 нм). При каком наибольшем расстоянии между диафрагмой и экраном в центре дифракционной картины еще будет наблюдаться темное пятно?
| Дано: D = 1,96 мм l = 600 нм | Решение
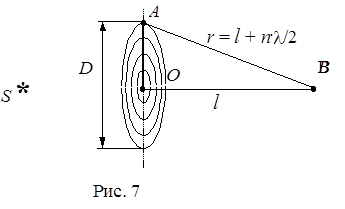
|
| l max –? |
Так как на диафрагму падает параллельный пучок монохроматического света, то фронт этих лучей – плоскость. Диафрагма будет вырезать из плоскости волнового фронта кружок диаметром D, в котором укладывается определенное число (n) зон Френеля. Расстояние АВ = r = l + n . l/2.
Из треугольника ОАВ
(l + n ·l/2) 2 = (D /2) 2 + l 2,
l 2 + l · n ·l + n 2. (l 2 /4) = D 2 /4+ l 2.
Ввиду малости величины l (l << l) величиной l 2 можно пренебречь, тогда
n = D 2 /(4 l l).
Последняя формула свидетельствует о том, что с увеличением расстояния между диафрагмой и экраном число зон Френеля, укладывающихся в отверстии диафрагмы, изменяется. От того, четное или нечетное число зон Френеля укладывается в отверстии диафрагмы, зависит результат дифракции: при четном числе наблюдается минимум, при нечетном – максимум.
Зависимость интенсивности света в центре дифракционной картины от расстояния между диафрагмой и экраном представлена на рис. 9.
| Из рис. 9 видно, что интенсивность максимумов падает, а интенсивность минимумов растет, приближаясь к интенсивности при полностью открытом фронте (n ®¥). При приближении к диафрагме | 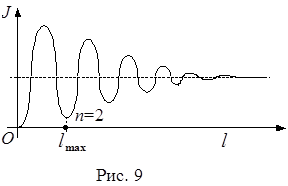
|
последний минимум наблюдается при числе открытых зон Френеля n =2, это соответствует искомому расстоянию l max. Подставляя значение n =2 в последнюю формулу, получим
2 = D 2 /(4 l max l), откуда l max = D 2 /(8 l).
l max = (1,96) 2. 10 ‑6 /(8 6 . 10 ‑7) =0,8 (м).
Ответ: l max = 0,8 (м).
Задача 8. На дифракционную решетку шириной 1 см падает нормально белый свет. Спектр проектируется линзой на экран, отстоящий от решетки на 3 м. Ширина спектра первого порядка 66 см. Определить: 1) постоянную решетки; 2) общее число главных максимумов, даваемых решеткой; 3) разрешающую способность решетки для максимума наибольшего порядка. Границы видимости спектра l кр = 780 нм, l ф = 400 нм.
| Дано: L =1 см=10‑2 м F =3 см=3.10‑2 м lкр=780 нм=7,80.10–7м lф = 400 нм=4.10–7м | Решение
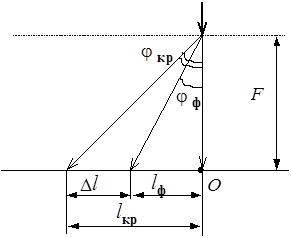 Рис. 10
Рис. 10
|
| 1) d –? 2) N –? 3) R –? |
На рис.10 j ф – угол дифракции, соответствующий углу отклонения от первоначального направления фиолетовых лучей, j кр – красных лучей. В точке О (центре дифракционной картины) собираются лучи, прошедшие дифракционную решетку без отклонения (j=0). В этой точке наблюдается центральный дифракционный максимум.
l ф – расстояние от центрального максимума до фиолетовой линии первого порядка, l кр – до красной линии; D l – длина спектра первого порядка. Так как углы дифракции первого порядка малы, можно считать, что
sin j» tg j» j (рад).
Из рисунка видно, что
j ф» l ф / F; j кр» l кр / F; D l = l кр – l ф = F (j кр – j ф).
Постоянная решетки d, длина волны l и угол дифракции j связаны между собой соотношением
d ×sinj = k ×l (условие главного максимума),
где k – порядок максимума.
По условию задачи k =1, sinj» j = l/ d.
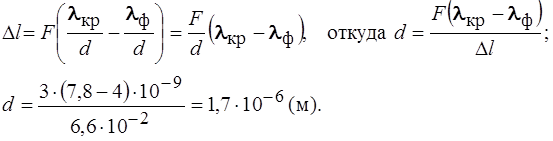
Общее число главных максимумов, даваемых решеткой, определяется максимальным порядком k max и равно N max =2 k max +1, так как дифракционная картина симметрична: число максимумов справа от центрального, слева от центрального и сам центральный максимум. Максимальный порядок, даваемый решеткой, получим из условия дифракционного максимума, положив sinj = 1, так как угол отклонения лучей решеткой не может превышать 90 ˚, при этом
k max = d /l min; k max =1,7 . 10 ‑6 /4 . 10 –7 =4,(25), то есть максимальный порядок равен 4 (всегда округляем в сторону уменьшения, так как максимум следующего порядка не виден).
Общее число главных дифракционных максимумов
N max = 2 . 4 + 1 =9.
Разрешающая способность дифракционной решетки определяется соотношением
R = k . N,
где N – общее число штрихов (щелей) решетки, k – порядок дифракционного максимума.
По условию задачи k = k max = 4. Число щелей найдем из ширины L дифракционной решетки, так как L = N . d,
N = L / d.
R = k max . L / d;
R = (4 . 10–2)/(1,7 . 10 –6) = 23529.
Ответ: d = 17 мкм, N max = 9, R = 23529.
Задача 9. Минимальное значение угловой дисперсии некоторой дифракционной решетки D =1,266 . 10 –3 рад/нм. Найти угловое расстояние между линиями с l 1 =480 нм и l 2 =680 нм в спектре первого порядка.
| Дано: D =1,266.10–3 рад/нм l1=480нм=4,8.10–7 м l2=680нм=6,8.10–7 м k =1 | Решение Угловое расстояние между линиями равно разности углов дифракции, соответствующих этим линиям Dj = j2 – j1. |
| Dj –? | Угловая дисперсия определяется соотношением D = k /(d . cos j). |
Минимальное значение угловой дисперсии соответствует минимальному значению k =1 и максимальному значению cos j =1, то есть
D min =1/ d,
следовательно, можно определить период решетки
d =1/ D min;
d =1/ 1,266 . 10 ‑6 =7,9 . 10 ‑7 (м).
Из условия дифракционного максимума
d sin j 1 = l 1 (k =1 по условию задачи)
d sin j 2 = l 2
sin j 1 = l 1 / d =4,8 . 10 ‑7 /7,9 . 10 ‑7 =0,6; j 1» 37˚;
sin j 2 = l 2 / d =4,8 . 10 ‑7 /7,9 . 10 ‑7 =0,6; j 2» 59˚;
Dj = 59˚ – 37˚=22˚.
Ответ: Dj = 22˚.
Задача 10. Будут ли разрешены дифракционной решеткой, имеющей 100 штрихов, спектральные линии с длиной волн l 1 =598нм и l 2 = 602 нм в спектре а) первого б) второго порядка?
| Дано: N =100 l1=598нм=5,98.10‑7м l2=602нм=6,02.10‑7м k =1, k =2 | Решение Разрешающая способность дифракционной решетки R ==l/(d×l)= k × N, (1) где d×l – наименьшая разность длин волн двух спектральных линий, при которой эти линии могут быть видны раздельно в спектре, |
| R –? | полученном посредством данной решетки. |
Если разность длин волн Dl < dl, две линии сливаются в одну, то есть не разрешаются дифракционной решеткой.
Для порядка k =1 R 1 =1 . 100=100, для порядка k =2 R 2 =2 . 100=200.
В формуле (1) Dl =l 2 – l 1 =602 – 598 = 4 (нм);
l =(l 2 + l 1)/2 = 600 (нм);
l /Dl = 600(нм)/4(нм)=150, что больше R 1 и меньше R 2.
Это означает, что для первого порядка Dl < dl и указанные в условии задачи линии не разрешаются данной дифракционной решеткой.
Для второго порядка Dl > dl и линии видны раздельно.
Ответ: а) не разрешены; б) разрешены.
Date: 2015-05-18; view: 6744; Нарушение авторских прав