
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Примеры решения задач. Задача 1. На пути луча рис.1, идущего в воздухе, поставили стеклянную пластинку толщиной h=1 мм
|
|
Задача 1. На пути луча рис.1, идущего в воздухе, поставили стеклянную пластинку толщиной h =1 мм. Насколько изменится оптическая длина пути луча, если луч будет падать на пластинку (n ст =1,5):
1) нормально;
2) под углом 30 ˚.
| Дано: h =1 мм i 1=0 i 2=30˚ n ст =1,5 | Решение В первом случае луч на границе воздух-стекло не преломляется и проходит в стекле путь, равный h. Когда луч шел в воздухе, его оптический путь L был равен его геометрическому пути L 1, так как показатель преломления воздуха n = 1. |
| D L –? | Стеклянная пластина изменяет оптическую длину пути, которая теперь складывается из геометрической длины пути (L 1– h) луча в воздухе и |
оптической длины пути nh в пластинке.
L 2 =(L 1 – h)+ nh = L 1 + h (n – 1).
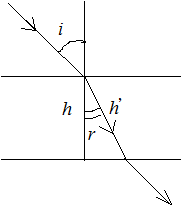
|
Изменение оптической длины пути будет равно
D L = L 2 – L 1 = L 1 + h (n – 1) – L 1 = h (n – 1).
D L = 1×(1,5–1)=0,5 (мм).
Во втором случае луч, падая на пластинку, будет преломляться, то есть проходить в пластинке путь h ΄ ¹ h, который найдем, пользуясь законом преломления
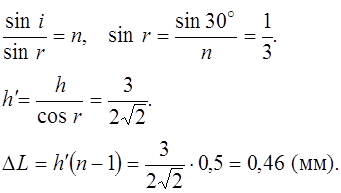
Ответ: 1) D L =0,5 мм, 2) D L =0,46 мм.
Задача 2. От двух когерентных источников S 1 и S 2 (l=0,8 мкм) лучи попадают на экран, на котором наблюдается интерференционная картина. Когда на пути одного из лучей перпендикулярно ему помещается мыльная пленка (n =1,33), интерференционная картина изменяется на противоположную. При какой наименьшей толщине пленки это возможно?
| Дано: l=0,8 мкм n =1,33 | Решение Изменение интерференционной картины на противоположную означает, что на тех участках экрана, где были интерференционные максимумы, стали наблюдаться минимумы и наоборот. Такое изменение интерференционной картины возможно при изменении оптической разности хода лучей S 1 и S 2 на нечетное число полуволн (l/2), то есть |
| d min–? |
D 2–D 1= (2 k + 1)l/2,
где D1 – оптическая разность хода лучей до внесения пленки, D2 – оптическая разность хода тех же лучей после внесения пленки;
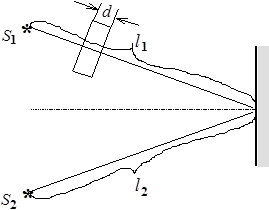
|
(k =0, ±1, ±2,...).
Наименьшей толщине пленки соответствует k =0. При этом предыдущая формула примет вид
D 2–D 1= l/2. (1)
Из рис. 2 видно, что D 1 = l 1 – l 2.
При внесении пленки оптический путь первого луча увеличивается на d min(n – 1), то есть
D 2 = D 1 + d min (n ‑1) и D 2 – D 1 = d min (n –1) (2)
Сравнивая соотношения (1) и (2), получим
d min ×(n – 1) = l /2,
откуда
d min = l /(2×(n – 1));
d min = 0,8 /(2×(1,33 – 1))=1,21 (мкм).
Ответ: d min = 1,21 мкм.
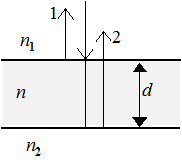
Задача 3. Плоскопараллельная стеклянная пластинка толщиной 1,2 мкм и показателем преломления n =1,5 помещена между двумя средами с показателями преломления n 1 и n 2 рис. 3. Свет с длиной волны l=0,6 мкм падает нормально на пластинку. Определить результат интерференции световых лучей 1 и 2, отраженных от верхней и нижней поверхностей пластинки, в следующих случаях:
1) n 1 < n < n 2; 2) n 1 > n > n 2; 3) n 1 < n > n 2; 4) n 1 > n < n 2.
d = 1,2 мкм; n = 1,5; l= 0,6 мкм 1) n 1 < n < n 2; 2) n 1 > n > n 2; 3) n 1 < n > n 2; 4) n 1 < n < n 2 | Решение
| |||
| max –?, min –? |
Результат интерференции зависит от оптической разности хода D интерферирующих лучей 1 и 2, другими словами, от числа полуволн l/2, укладывающихся на оптической разности хода:
если 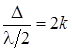 (четное число), то наблюдается усиление света (интерференционный максимум),
(четное число), то наблюдается усиление света (интерференционный максимум),
если 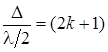 (нечетное число), то происходит ослабление света (интерференционный минимум).
(нечетное число), то происходит ослабление света (интерференционный минимум).
При определении оптической разности хода надо учитывать, что при отражении от оптически более плотной среды появляется дополнительная разность хода l/2, обусловленная изменением в этом случае фазы колебаний на p.
Таким образом, при нормальном падении света на пластинку, оптическая разность хода лучей 1 и 2 будет равна D= 2 dn + (l/2), если один из лучей отражается от оптически более плотной среды, или D= 2 dn, если оба луча отражаются от оптически более плотной среды или оба луча отражаются от оптически менее плотной среды.
Учитывая сказанное выше, получим для четырех случаев:
1) D= 2 dn; 2) D= 2 dn; 3) D= 2 dn + (l/2); 4) D= 2 dn + (l/2).
В первых двух случаях
D= 2×1,2×1,5=3,6 (мкм);
l/2=0,6/2=0,3 (мкм).
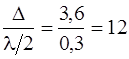 – четное число, наблюдается усиление света.
– четное число, наблюдается усиление света.
В третьем и четвертом случаях
D= 2×1,2×1,5+0,3=3,9 (мкм).
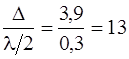 – нечетное число, наблюдается ослабление света.
– нечетное число, наблюдается ослабление света.
Ответ: 1) max; 2) max; 3) min; 4) min.
Задача 4. Поверхности стеклянного клина образуют между собой угол 0,2 ΄. На клин нормально падает пучок лучей монохроматического света с длиной волны 0,55 мкм. Определить ширину интерференционной полосы рис.4.
| Дано: a=0,2΄=5,8×10‑5 рад l= 0,55 мкм. | Решение Как и в случаях плоскопараллельной пластинки, интерферируют лучи 1 и 2, отраженные от верхней и нижней грани клина. |
| l –? |
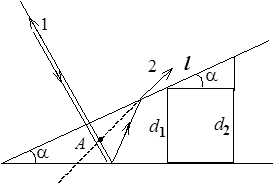
|
Интерференционные полосы (полосы равной толщины) наблюдаются у поверхности клина (интерференция лучей 1 и 2 произойдет в точке А).
Ширина интерференционной полосы – это расстояние между двумя соседними темными полосами (минимумами k –го и (k +1)–го порядков). Темные полосы будут наблюдаться на тех участках клина, где выполняется условие
D1, 2 = (2 k +1)×l/2.
Воспользуемся формулой
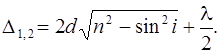
Для нормального падения лучей (i =0)
D = 2 dn +×l/2,
следовательно, условие минимума:
2 dn + l/2 = (2 k + 1) ×l/2
или
2 dn = k ×l.
Предположим, что толщина клина, соответствующая максимуму k –го порядка равна d 1, а максимуму (k +1)–го порядка – d 2, тогда
2 d 1 n = k ×l;
2 d 2 n = (k + 1) ×l.
Решая систему уравнений, получаем
d 2 – d 1= l /(2 n).
Из рисунка видно, что d 2 – d 1= l sin q.
Ввиду малости угла q (по условию q = 0,2 ΄) sin q» q (рад), следовательно,
d 2 – d 1= l × q = l/(2 n) и l =l/(2 n q);
l = (5,5 ×10 ‑7) / (2×1,5×5,3 ×10 ‑5) = 0,00315 (м).
Ответ: l = 0,00315 (м).
Задача 5. Установка для наблюдения колец Ньютона освещается нормально падающим монохроматическим светом (l=500 нм). Пространство между линзой и стеклянной пластинкой заполнено сероуглеродом (n =1,6). Радиус кривизны линзы 10 м. Показатель преломления линзы и пластины равны, соответственно, 1,5 и 1,7. Определить радиус третьего темного кольца Ньютона рис.5.
| Дано: l =500 нм = =5×10‑7 м R = 10 м n = 1,6 n 1 = 1,5 n 2= 1,7 | Решение
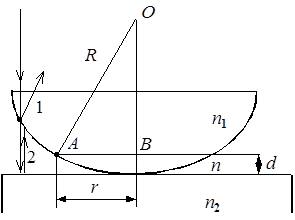
|
| r 3 –? |
В установке по наблюдению колец Ньютона на стеклянную пластинку положена плосковыпуклая линза большого радиуса кривизны R. Между линзой и стеклянной пластинкой возникает тонкий воздушный зазор, заполненный (по условию задачи) жидкостью с показателем преломления n. В этом тонком жидком слое переменной толщины происходит интерференция лучей 1 и 2, отраженных от верхней и нижней поверхностей пленки. Наблюдаются в данном случае полосы равной толщины, представляющие собой кольца радиуса r (см. рисунок), соответствующие толщине слоя d. Так как n > n 1, то луч 1 отражается от оптически более плотной среды, следовательно, при отражении происходит изменение фазы колебаний луча 1 на p (потери полуволны). Но n 2 также больше n, следовательно, и луч 2 отражается от оптически более плотной среды и при отражении также происходит потеря полуволны. Оптическая разность хода лучей 1 и 2 определяется следующим соотношением с учетом нормального падения лучей и сказанного выше
D = 2 dn – l/2 + l/2 = 2 dn.
Из D АОВ на рисунке следует, что
R 2 = (R – d)2 + r 2 = R 2– 2 Rd + d 2 + r 2 …
Ввиду малой толщины зазора между линзой и стеклянной пластинкой величиной d 2 можно пренебречь, тогда
r 2 = 2 Rd, r = 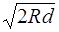 .
.
Так как по условию задачи надо определить радиус темного кольца, применим условие интерференционного минимума
D= 2 dn = (2 k + 1) ×l/2, откуда d = [(2 k + 1) ×l] / (4 n),
и r = 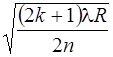 .
.
По условию задачи k = 3
r = 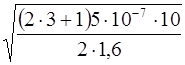 =1,04 . 10 –3 (м).
=1,04 . 10 –3 (м).
Ответ: r =1,04 . 10 –3 (м).
Date: 2015-05-18; view: 24118; Нарушение авторских прав