Измерение эффективности

На рис. 3.1 показаны ежегодное число удачных попыток Микки забить мяч с 1951 до 1968, и общее среднее число успешных попыток за это время. Эти числа показаны как

точки - «точечная оценка», а вертикальные тонкие линии дают «95-процентный доверительный интервал.» Эти две концепции очень важно понять в начале, потому что они будут применяться позже, чтобы показать, почему мы можем доверять результатам psi - экспериментов.

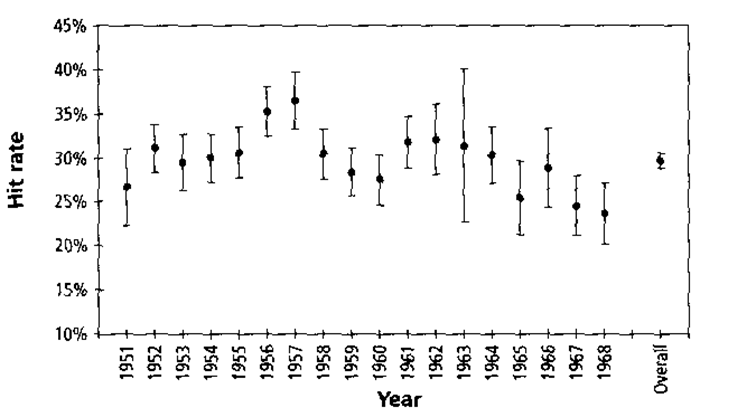
Рис. 3.1. Ежегодное и общее среднее число удачных попыток Микки

Мантла с 95% доверительным интервалом.

«Точечная оценка» - есть оценка удачных попыток, вычисленная как процентная доля из общего числа попыток за год. Это называется «точечной оценкой», потому что это число - одиночное значение, которое подразумевает высокую точность. Проблема состоит в том, что мы знаем, что в разные года общее число попыток забить мяч у Микки сильно изменялось. Так, в один год у него было только десять попыток, из которых были успешными восемь, и точечная оценка в этот год составила 80%. В следующем году у него было триста общих попыток из которых 100 закончились голами. Это дает оценку в 33%.

Если бы мы обратили внимание только на точечную оценку, то можно было бы думать, что искусство забивать мячи у Микки сильно изменяется от года к году. Но так как мы знаем, что в одном случае было вообще только 10 общих попыток, а в другом - 300, то мы понимаем, что оценка эффективности Микки в 80%, несмотря на точность вычисления цифры в 80%, не является хорошей мерой его долгосрочной результативности.

Поэтому, помимо собственно оценки эффективности — точечной оценки — мы нуждаемся в чем-то еще, чтобы оценить степень доверия, которую мы можем иметь для этой точечной оценки. Вот почему появляется «95% доверительный интервал». Небольшой доверительный интервал для данной точки, означает, что эта точечная оценка основана на большом количестве испытаний, или что повторные наблюдения были очень близки друг к другу, или даже одинаковы. Большой интервал доверия означает, что точечная оценка была основана на небольшом количестве испытаний, или повторные наблюдения сильно отличались от друг друга. Определение «95% доверительный интервал» - означает, что мы можем на 95% процентов уверены в том, что действительная, долгосрочная оценка результативности существует где-то в этом диапазоне.

На рис. 3.1 мы видим, что эффективность Микки широко менялась за эти годы, как по уровню точечных оценок, так и по уровню доверительного интервала. В 1960 например, эффективность Микки составила 27% и мы полагаем, что эта оценка отражает уровень его бейсбольного искусства, потому что 95% интервал составляет величину от приблизительно 24% до 30%.

Мы можем думать, что у него было в этом году или общее большое количество попыток или результативность каждой его игры (при относительно небольшом их общем числе) была примерно одинакова. Напротив, в 1963, на первый взгляд, он как будто бы играл лучше, чем в 1960, потому что его точечная оценка составила 32%. Но, обращая внимание на 95% доверительный интервал, мы видим, что он или вообще мало играл в этом году или результативность каждой попытки забить мяч широко изменялась, так что эффективность его игры располагается где-то между 22% и 40%.

Теперь отметим другой важный момент: поскольку два 95% доверительных интервала для оценки эффективности игры Микки в 1960 и 1963 г. перекрываются, мы не можем с уверенностью сказать, что уровень игры Микки сильно различался в эти годы. Другими словами, совершенно верно, что в среднем эффективность игры Микки составила 27% в 1960 и 32% в 1963, но мы имеем низкую степень доверия к тому, что эти 5 процентов различия (32% минус 27%) отражают подлинное различие уровня эффективности игры Микки. Эти 5% вполне могут объясняться случайными колебаниями, не связанными с уровнем игры.Статистик сказал бы, что в этом случае различие двух оценок несущественно. Высказывание, что два значения отличаются «существенно» означает, что, в соответствии с соглашением, мы имеем, по меньшей мере, 95% уверенность в том, что эти две наблюдаемых оценки отражают реальные основные различия. Это заключение, в свою очередь, эквивалентно высказыванию, что можно поставить двадцать шансов против одного, что различие существует в действительности.

Теперь мы подготовлены к другой важной концепции. Заметим, что в правой стороне рис. 3.1 «общий» рейтинг Микки показан величиной в 29%, с очень маленьким доверительным интервалом. Это говорит нам с 95% достоверностью, что его фактическая эффективность игры за все время была где-то между 27 и 31%. Рассматривая данные за все время, мы можем оценить истинное умение Микки забивать мячи в доверительном интервале размером всего в 3 - 4%. А для любого данного года мы имели доверительный интервал этой оценки величиной от 5 до 10%. Таким образом, объединение данных увеличивает наше доверие к измеряемой величине или уменьшает доверительный интервал.

Date: 2015-05-18; view: 655; Нарушение авторских прав