Потенциал и напряженность поля системы точечных зарядов

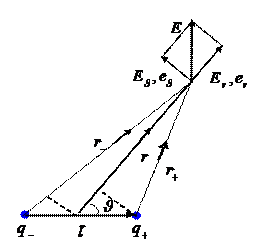
7.1. Потенциал и напряженность поля электрического диполя.

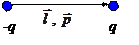Точечным электрическим диполем называется система, состоящая из двух одинаковых по величине разноименных точечных зарядов, расстояние 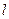между которыми значительно меньше расстояния до точки, где определяется поле системы.

Вектор 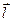проводится от отрицательного заряда к положительному. Так же направлен электрический дипольный момент 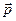системы электрических зарядов:

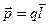. (7.1)

Для нахождения поля электрического диполя,

в силу осевой симметрии рассматриваемой системы

достаточно определить электрическое поле в плоскости,

проходящей через ось диполя .

Найдем сначала потенциал электрического поля диполя:

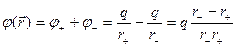(7.2)

При 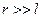можно записать

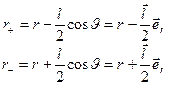
и 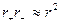, тогда

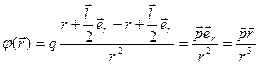. (7.3)

или иначе (в полярных координатах):

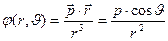. (7.4)

Из (7.4) следует, что потенциал поля диполя убывает с расстоянием быстрее, чем потенциал поля точечного заряда (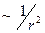 вместо ).

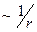Вектор напряженности удобно представить в виде суммы компонент вдоль ортов 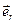и :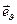

,

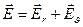Для нахождения напряженности поля электрического диполя воспользуемся формулой (6.10):

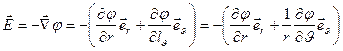, (7.5)

где 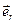и 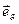– единичные векторы двух взаимно перпендикулярных направлений (см. рис.).

тогда модули компонент равны

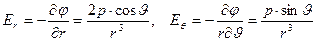. (7.6)

Модуль вектора :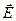

.

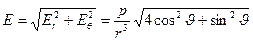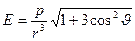. (7.7)

Вектор напряженности электрического поля точечного диполя можно представить в следующей полезной форме:

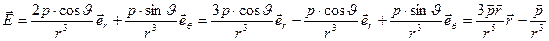, (7.8)

поскольку

.

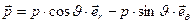
7.2. Диполь во внешнем электрическом поле.

1) Однородное поле вектора :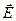

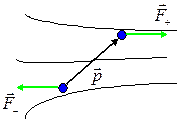
Сумма сил, действующих на диполь со стороны поля, равна нулю (см. рисунок), т.к. модули действующих на заряды сил равны, а направления этих сил противоположны:

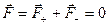, (7.9)

однако момент сил, стремящийся повернуть диполь вдоль направления поля, вообще говоря, отличен от нуля:

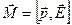. (7.10)

Этот момент сил стремится повернуть диполь таким образом, чтобы его электрический момент 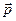установился по направлению внешнего поля 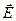. Такое положение диполя во внешнем электрическом поле является устойчивым. Как мы увидим ниже, именно такая ориентация диполя обеспечивает минимум его потенциальной энергии.

2) Неоднородное поле:

Силы, действующие на заряды диполя в таком поле различны и результирующая сила уже не равна нулю:

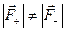и .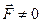

Силу можно вычислить как градиент потенциальной энергии диполя: 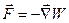. Энергию диполя в электрическом поле находим как сумму энергий каждого из образующих его точечных зарядов:

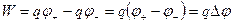
Считая 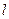малой величиной (фактически усредняя поле на длине диполя), можно записать

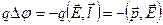
Таким образом, потенциальная энергия точечного диполя:

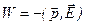. (7.11)

Выражение (7.10) определяет энергию точечного диполя в любом электрическом поле. При этом здесь не учитывается энергия взаимодействия зарядов, образующих диполь, между собой.

Очевидно, что минимум энергии рассматриваемой электрической системы (диполя) достигается в том случае, когда диполь ориентирован по полю.

Для силы, определенной как градиент потенциальной энергии, имеем

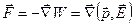. (7.12)

Для вычисления градиента от скалярного произведения векторов воспользуемся известной формулой векторного анализа:

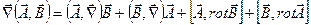. (7.13)

Подставляя вместо 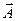и 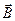векторы 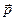и 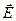, соответственно, получаем

.

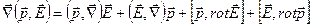Очевидно, что в правой части последнего выражения все слагаемые, кроме первого, равны нулю. В самом деле, и 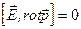из-за того, что дипольный момент 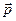есть величина постоянная; 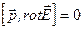поскольку рассматриваемое электрическое поле потенциально: .

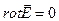Т. о., для силы, действующей на точечный диполь, получаем следующее выражение:

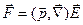. (7.14)

Пример: частный случай - пусть ось 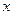направлена вдоль вектора 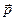(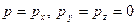), тогда получаем

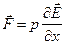. (7.15)

Момент сил, действующих на диполь, как и в однородном поле, определяется выражением (7.10). Поэтому в неоднородном электрическом поле диполь будет вести себя следующим образом: под действием момента сил диполь будет стремиться установиться по полю (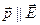), а результирующая сила будет перемещать его в направлении увеличения модуля 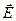. Оба движения будут совершаться одновременно.

7.3. Поле, создаваемое системой зарядов на больших расстояниях.

Рассмотрим систему, состоящую из 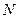зарядов 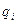, находящихся внутри области с линейными размерами порядка .

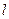Найдем электрическое поле, создаваемое такой системой на больших расстояниях: .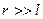

Потенциал, создаваемый системой на расстоянии 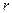, равен

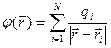. (7.16)

Учтем, что , и приближенно запишем знаменатель в (7.16) в виде:

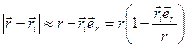(7.17)

Теперь, учитывая также, что

,

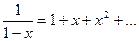где ,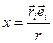

разложим потенциал (7.16) в ряд:

(7.18)

Обсудим отдельные слагаемые, входящие в выражение (7.18).

а) 1-ое слагаемое описывает потенциал точечного заряда 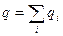(иначе - монополь).

.

б) Во 2-ом слагаемом можно выделить дипольный электрический момент системы зарядов:

(7.19)

Таким образом, 2-ое слагаемое описывает потенциал, создаваемый дипольным моментом рассматриваемой системы зарядов:

.

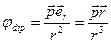Если система электронейтральна, т.е. 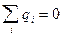, то поле создается только дипольным моментом системы. Интересно отметить, что дипольный момент не зависит от выбора начала отсчета. В самом деле, пусть имеются две системы координат с началами в точках 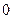и 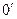, отстоящие друг от друга на расстояние 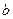, тогда 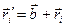и, поскольку 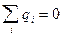, имеем

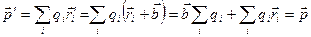. (7.20)

Если 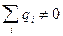, то основной вклад на больших расстояниях дает суммарный заряд системы - монополь.

Если же система электронейтральна, то создаваемое ею на больших расстояниях электрическое поле, определяется, главным образом, дипольным моментом системы.

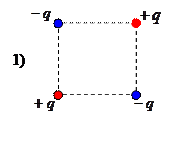Если полный заряд и дипольный момент системы равны нулю: 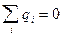и 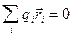, то основной вклад дают другие мультипольные моменты: в первую очередь – квадруполь,

поле которого убывает с расстоянием как 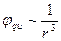, или октуполь,

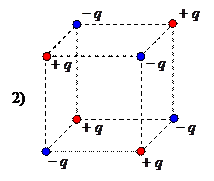
для которого 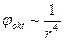и т.д.

Такое представление поля системы зарядов называется разложением по мультиполям. Его можно провести и для непрерывного распределения зарядов.

Примеры квадруполя (заряд и дипольный момент такой системы равны нулю) и октуполя (у которого заряд, дипольный и квадрупольный моменты равны нулю) показаны на рисунках 1) и 2), соответственно.

Date: 2015-05-09; view: 1691; Нарушение авторских прав