Дифференциальная форма теоремы Гаусса

4.1. Дивергенция вектора 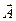в декартовой системе координат.

Рассмотрим некоторую точку 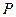, принадлежащую объему , в поле произвольного вектора .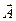

Определим удельную мощность источников поля вектора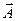

(векторного поля) в точке 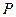следующим образом:

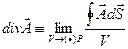, (4.2)

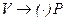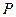где означает, что объем стягивается к точке , или .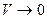

Выражение (4.2) является математическим определением дивергенции вектора .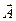

Т.о., дивергенцией вектора 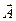в данной точке называется предел, к которому стремится отношение потока вектора 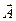через малую произвольную замкнутую поверхность 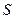, окружающую эту точку, к величине ограниченного этой поверхностью объема при .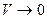

Выражение для дивергенции будет зависеть от выбора системы координат.

Сосчитаем дивергенцию векторного поля 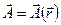в декартовой системе координат. Для этого построим параллелепипед с вершиной в точке 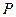с координатами 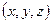и ребрами 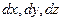, ориентированными вдоль соответствующих осей. Векторное поле в точке 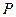запишем как

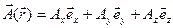. (4.3)

Найдем поток вектора через поверхность параллелепипеда как сумму потоков через его грани:

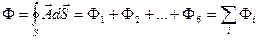. (4.4)

Вычислим поток вектора через грань 1

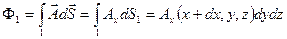, (4.5)

где вектор 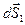направлен вдоль оси 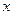, а по модулю равен 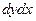. Найдем теперь поток, выходящий через грань 2, которая расположена с противоположной грани 1 стороны “кубика”:

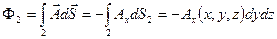(4.6)

В последнем выражении знак «минус» появился из-за противоположного по отношению к оси 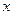направления вектора 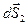. Суммарный поток, выходящий из “кубика” через грани 1 и 2, равен

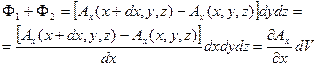(4.7)

Аналогично получаем потоки через пары других параллельных граней:

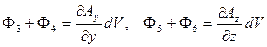. (4.8)

Суммируя (4.7) и (4.8), получаем суммарный поток через поверхность маленького параллелепипеда:

. (4.9)

Откуда удельная мощность источников электрического поля:

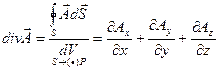. (4.10)

Дивергенция вектора 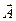, т.е. 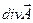, является, как и поток 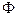, скалярной величиной.

Дивергенция может быть определена посредством векторного оператора набла

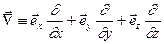(4.11)

как операция скалярного умножения оператора 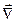на вектор поля, например, на вектор :

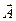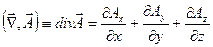. (4.12)

Примечание. Пусть имеем векторное поле .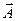

Определения:

1) Те точки поля вектора 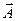, где 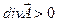, называются истоками поля, при этом модуль дивергенции дает

мощность истока.

2) Те точки поля, где 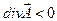– стоки поля.

3) Векторное поле, в котором во всех точках 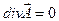, – поле свободное от источников, иначе,

соленоидальное.

В применении к электрическому полю мы доказали теорему Гаусса в интегральной форме (3.8) или (3.9). Разделим эти уравнения на объем , ограниченный поверхностью 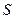, и, стягивая этот объем к интересующей нас точке 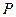, находящейся внутри (устремляя 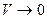), получаем в левых частях уравнений дивергенцию вектора 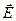, а в правых – плотность электрического заряда в точке .

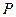Итак, теорема Гаусса в дифференциальной форме (для электрического поля):

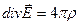(4.13)

Это – одно из системы уравнений Максвелла в дифференциальной форме, записанное для поля в вакууме.

Примечание. В СИ имеем .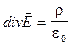

4.2. Теорема Остроградского-Гаусса.

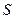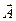Пусть произвольная замкнутуя поверхность ограничивает некоторый объем в поле вектора . Разобьем этот объем на систему бесконечно маленьких кубиков и сложим потоки через грани этих кубиков (пусть 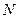- число граней). Т.к. потоки через внутренние грани кубиков в сумме равны нулю, полный поток определяется суммированием (в пределе – интегрированием) по внешней поверхности 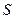рассматриваемой области, а дивергенция – интегрированием по объему всех кубиков:

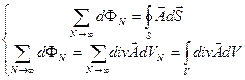(4.14)

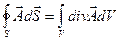(4.15)

Уравнение (4.15) выражает теорему Остроградского-Гаусса, справедливую для любого векторного поля .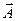

Теорема Остроградского-Гаусса. Поток вектора 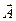через произвольную замкнутую поверхность равен интегралу от дивергенции вектора 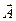по объему, ограниченному этой поверхностью.

Математическая формула (4.15) позволяет при проведении вычислений выразить поток вектора через произвольную замкнутую поверхность через объемный интеграл по области, ограниченной этой поверхностью.

Эта формула часто применяется в теории электричества и других разделах теоретической физики.

Теорема Ирншоу. В сякая равновесная конфигурация покоящихся точечных электрических зарядов неустойчива, если отсутствуют какие-либо силы, кроме кулоновских.

Эта теорема является следствием теоремы Гаусса. В самом деле, если на рассматриваемый

заряд 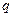действует сила со стороны других зарядов, но этот заряд находится в равновесии, то

действующая на него суммарная сила равна нулю и, следовательно, поток вектора 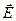через

поверхность, окружающую заряд, также равен нулю. Если равновесие устойчиво, то при

смещении заряда должна возникать возвращающая сила, характеризуемая вектором 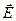, т.е. должен возникнуть поток вектора напряженности электрического поля, отличный от нуля, что противоречит теореме Гаусса.

Date: 2015-05-09; view: 837; Нарушение авторских прав