Потенциал электростатического поля

6.1. Потенциал.

Наряду с описанием электрического поля с помощью его силовой характеристики – вектора 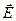, возможен и другой адекватный способ описания – энергетический.

Для потенциальных полей, создаваемых неподвижными электрическими зарядами, можно ввести понятия потенциальной энергии, потенциала и разности потенциалов.

Потенциал электростатического поля 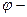энергетическая характеристика этого поля. Потенциал определен с точностью до аддитивной постоянной. Значение этой постоянной не играет роли, поскольку поведение частиц или тел в электрических полях определяется не абсолютными значениями потенциалов, а их разностями между различными точками пространства. Поэтому потенциалу какой-либо произвольной точки поля 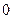можно приписать для определенности любое значение .

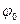В теоретической физике за нулевой потенциал принимают потенциал бесконечно удаленной точки пространства 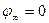. На практике за нулевой потенциал обычно принимают потенциал Земли.

Потенциал поля точечного заряда:

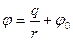, (6.1) где 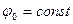- значение потенциала, от которого ведется отсчет, или, положив ,

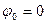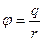. (6.2)

Примечание. В СИ потенциал точечного заряда: .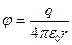

Потенциальная энергия 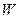заряда 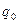в электростатическом поле определяется через потенциал 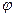как

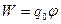. (6.3)

Согласно (6.3) потенциал какой-либо точки поля можно определить как величину, численно равную потенциальной энергии единичного положительного заряда в данной точке поля.

С учетом (6.2) и (6.3) выражение (5.2), полученное в предыдущем параграфе для работы сил поля покоящегося точечного заряда, можно записать

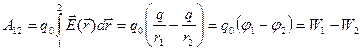, (6.4)

где 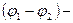разность потенциалов между точкам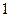и и 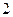, 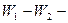убыль потенциальной энергии.

Разность потенциалов 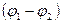между точкам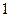и и 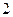определяют как работу, совершаемую силами поля при перемещении единичного положительного заряда по произвольному пути из точки 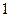в точку .

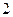Такое определение имеет смысл именно потому, что работа электростатического поля не зависит от формы пути, а определяется только положениями его начальной и конечной точек.

Из (6.4) следует, что разность потенциалов между двумя произвольными точками электростатического поля можно записать как

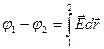, (6.5)

откуда можно заключить, что в электрическом поле существует некоторая скалярная функция координат 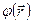, убыль которой определяется выражением (6.5).

Система электрических зарядов.

Из принципа суперпозиции следует, что свойство потенциальности справедливо для электрического поля любой системы или конфигурации неподвижных зарядов. Поэтому потенциал поля, создаваемого системой зарядов (точечных), определяется выражением:

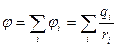. (6.6)

В случае непрерывно распределенного заряда на поверхности или в некоторой области пространства потенциал определяется выражениями:

если известна поверхностная плотность заряда ,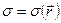

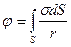, (6.7)

если задана объемная плотность заряда ,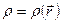

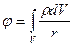. (6.8)

Единицы потенциала: в системе 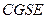единица потенциала выбирается исходя из (6.2) - 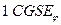. В системе СИ единица потенциала есть Вольт: 1 В = 1 Дж×Кл^-1.

Связь между единицами:

.

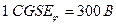6.2. Связь напряженности и потенциала. Уравнение Пуассона.

Из курса механики известно, что сила, действующая на частицу в поле, определяется как градиент потенциальной энергии частицы в этом поле

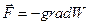. (6.9)

Пользуясь определениями (2.5) и (6.3), находим связь между потенциалом и напряженностью поля:

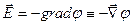. (6.10)

Возьмем дивергенцию от обеих частей уравнения (6.10)

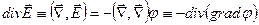. (6.11)

Распишем теперь скалярное произведение векторных операторов «набла»:

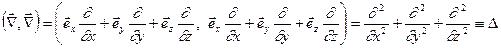. (6.12)

Выражение (6.12) определяет оператор Лапласа .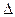

Воспользуемся теперь теоремой Гаусса для вектора 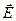в дифференциальной форме (4.13):

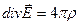
Сравнивая выражения (6.11) и (4.13), получаем уравнение Пуассона, определяющее связь между пространственным распределением заряда (плотностью заряда 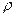) и потенциалом :

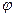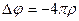, (6.13)

Или

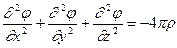. (6.14)

Это одно из основных уравнений электростатики, которое позволяет найти потенциал электрического поля по заданному распределению (плотности) заряда.

Теорема единственности.

В теории доказывается, что уравнение (6.13) имеет единственное решение. Это утверждение называют теоремой единственности.

Решение уравнения (6.13) в общем случае – сложная и кропотливая задача. Аналитические решения этого уравнения получены лишь для немногих частных случаев. Использование же теоремы единственности существенно облегчает решение целого ряда электростатических задач. Смысл теоремы единственности можно сформулировать следующим образом: если решение задачи удовлетворяет уравнению Пуассона и граничным условиям (их мы обсудим в следующей главе), то можно утверждать, что оно является правильным и единственным, каким бы способом (например, путем догадки) мы ни нашли его.

С физической точки зрения содержание теоремы единственности довольно очевидно: если предположить, что возможно не одно решение задачи, то существует не единственный потенциальный «рельеф», следовательно, в каждой точке пространства поле 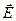определено, вообще говоря, не однозначно, т.е. мы приходим к физическому абсурду.

Date: 2015-05-09; view: 780; Нарушение авторских прав