
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Прямые произведения и функции
|
|
Прямым декартовым “х” множеством А и В называется множество всех пар (a;b), таких, что аÎА, bÎB.
С=AхВ, если А=В то С=А2.
Прямыми «х» n множеств A1x,…,xAn называется множество векторов (a1,…an) таких, что a1ÎA1,…, AnÎAn.
Через теорию множеств введем понятие функции.
Подмножество FÎMx x My называется функцией, если для каждого элемента хÎMx найдется yÎМу не более одного.
(x;y)ÎF, y=F(x).
Соответствие между аргументом и функцией можно изобразить с помощью диаграммы Венна:
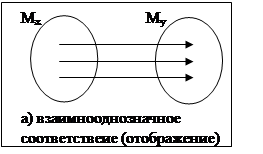 | |||
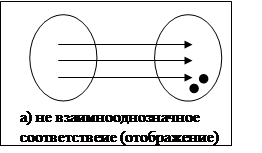 |
Определение: Между множествами MX и MY установлено взаимноодназночное соответствие, если каждому хÎMX соответствует 1 элемент yÎMY и обратное справедливо.
Пример: 1) (х,у) в круге
 |
 |
2) x = sinx
 |
Rà R
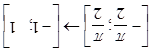
 |
Пусть даны две функции f: AàB и g: BàC, то функция y:AàC называется композицией функций f и g.
Y=f o g o – композиция.
Способы задания функций:
1) таблицы, определены для конечных множеств;
2) формула;
3) графики;
Способы 1-3 частные случаи выч. процедуры.
Пример процедуры, не относящейся к 3 способам задания функций n!
Взаимнооднозначное соответствие и мощности множеств.
Определение: Множества равномощны |A|=|B| если между ними взаимнооднозначное соответствие.
Теорема: Если для конечного множества А мощность равна |A| то количество всех подмножеств 2|A|=2n.
Множества равномощные N называются счетными, т.е. в них можно выполнить нумерацию элементов. N – множество натуральных чисел.
Множество N2 – счетно.
Date: 2015-04-23; view: 615; Нарушение авторских прав