
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Свойства операций над множествами
|
|
1. A 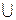 B = B
B = B 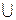 A; A
A; A 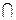 B = B
B = B 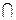 A – коммутативность.
A – коммутативность.
2. (A 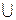 B)
B) 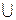 C =A
C =A 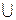 (B
(B 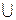 C), A
C), A 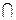 (B
(B 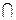 C)=(A
C)=(A 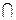 B)
B) 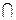 C – ассоциативность.
C – ассоциативность.
3. (A 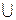 B)
B) 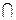 C = (A
C = (A 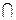 C)
C) 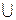 (B
(B 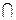 C), (A
C), (A 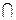 B)
B) 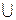 C=(A
C=(A 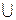 C)
C) 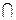 (B
(B 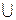 C) – дистрибутивность.
C) – дистрибутивность.
4. Поглощение A 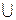 A = A, A
A = A, A 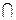 A = A.
A = A.
5. Существование универсальных границ.
А 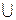 Ø = A; A
Ø = A; A 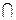 Ø = Ø; A
Ø = Ø; A 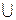 U = U; A
U = U; A 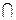 U = A
U = A
6. Двойное дополнение 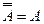
7. 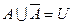
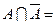 Ø
Ø
8. Законы двойственности или закон Де – Моргана
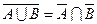
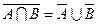
|
| ||||

Лекция 2: «Теория булевых функций. Булева алгебра»
Определение: Множество M с двумя введенными бинарными операциями (& V), одной унарной операцией ( ) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (аксиомы булевой алгебры). Названия операций пока не введены.
) и двумя выделенными элементами называется булевой алгеброй, если выполнены следующие свойства (аксиомы булевой алгебры). Названия операций пока не введены.
1. X & Y = Y&X, X V Y = Y V X – коммутативность.
2. (X & Y) & Z = X & (Y & Z), (X V Y) V Z = X V (Y V Z) – ассоциативность.
3. (X V Y) & Z = (X & Z) V (Y & Z), (X & Y) V (Y & Z) = (X V Z) & (Y & Z) – дистрибутивность.
4. Поглощение – X & X = X, X V X = X.
5. Свойства констант
X & 0 = 0
X & I = X, где I – аналог универсального множества.
6. Инвальтивность (двойное отрицание) 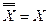 .
.
7. Дополнимость X V 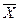 = I, X &
= I, X & 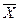 = 0.
= 0.
8. Законы двойственности – (X & Y)* = X* V Y*, (X V Y)* = X* & Y
Булева алгебра всех подмножеств данного множества.
U = {a1, a2… an)
[U] = N
[P(U)] = 2n
Легко показать, что свойства операций над множествами совпадают со свойствами (аксиомами) булевой алгебры. То есть, множество P(U) с операциями объединения, пересечения и дополнения является булевой алгеброй.
Oбъединение эквивалентно V, пересечение - &, дополнение -  , пустое множество – 0, а универсальное – I.
, пустое множество – 0, а универсальное – I.
Все аксиомы булевой алгебры справедливы в операциях над множествами.
Date: 2015-04-23; view: 780; Нарушение авторских прав