
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

ВВЕДЕНИЕ. Учебная дисциплина “Дискретная математика” предназначена для реализации государственных требований к содержанию и уровню подготовки выпускников по
|
|
Учебная дисциплина “Дискретная математика” предназначена для реализации государственных требований к содержанию и уровню подготовки выпускников по специальности “Программное обеспечение вычислительной техники и автоматизированных систем” для колледжа.
Преподавание данного курса имеет практическую направленность и проводится в тесной взаимосвязи с другими общепрофессиональными дисциплинами. Использование межпредметных связей обеспечивает преемственность изучения материала.
Материал данного предмета используется при изучении дисциплин “Математика и информатика”, “Математическая статистика”, “Архитектура ЭВМ, систем и сетей”, “Основы алгоритмизации и программирование”, “Базы данных”, “Автоматизированные системы”, “Технология разработки программных продуктов”, “Компьютерное моделирование”.
Рабочей программой дисциплины предусматривается изучение:
· основ теории множеств;
· систем счисления и модулярной арифметики;
· основ теории графов;
· основ комбинаторики;
· основ алгебры логики.
В результате изучения дисциплины студент должен:
иметь представление:
· о значении и областях применения данной дисциплины:
знать:
· основы теории множеств;
· аппарат формул логики и теорию булевых функций;
· способы минимизации логической схемотехники;
· основы алгебры вычетов;
· методологию шифрования;
· метод математической индукции;
· основные формулы комбинаторики;
· основы теории графов;
уметь:
· выполнять операции над множествами, применять аппарат теории множеств для решения задач;
· строить таблицы истинности для формул логики и упрощать формулы логики;
· представлять булевы функции в виде форму заданного типа, определять возможность выражения одних булевых функций через другие;
· исследовать бинарные отношения на заданные свойства;
· выполнять операции в алгебре вычетов;
· применять простейшие шифры для шифрования текстов;
· доказывать утверждения с помощью метода математической индукции;
· генерировать основные комбинаторные объекты;
· находить характеристики графов, выделять структурные особенности графов, исследовать графы на заданные свойства, применять аппарат теории графов для решения прикладных задач;
· строить автоматы с заданными свойствами.
Базовыми дисциплинами для изучения предмета “Дискретная математика” являются “Математика” и “Информатика”.
Рабочая программа учебной дисциплины на 90 часа аудиторных занятий, в том числе 24 часа отводится на практические занятия.
Лекция 1: «Множество. Алгебра множеств»
Введем обозначения:
N (или ω) –множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
R – множество действительных (вещественных) чисел;
С – множество комплексных чисел.
X  R – элемент X принадлежит множеству R.
R – элемент X принадлежит множеству R.
Равные множества – множества, состоящие из одинаковых элементов.
A = B – множество А равно множеству B.
Ø – пустое множество.
A 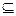 C – Множество А является подмножеством множества С.
C – Множество А является подмножеством множества С.
Если A 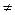 C и A
C и A 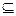 C, то A
C, то A 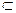 C (строго).
C (строго).
Если A 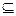 C и C
C и C 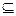 A, то A = С.
A, то A = С.
Пустое множество Ø является подмножеством любого множества.
Универсальное множество (универсум) U содержит в себе все множества и любое множество является подмножеством универсального множества.
Можно записать следующее: Ø 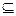 N
N 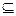 Z
Z 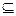 Q
Q 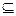 R
R 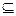 C
C 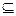 U.
U.
Множества A и B называются эквивалентными (обозначается A~B), если  биекция f: A↔B (или по другому y=f(x) и x=f(y), при y
биекция f: A↔B (или по другому y=f(x) и x=f(y), при y  A и x
A и x  B).
B).
Мощностью множества A называется класс всех множеств, эквивалентных множеству A (обозначается 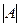 ).
).
Существуют конечные и бесконечные множества. Пусть множество A состоит из n элементов. Это множество называется конечным. Число n называется мощностью данного множества. 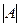 =n.
=n.
Множество натуральных чисел мощность является счетным (т.е. все элементы можно пронумеровать). Если A~N, то мощность 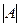 =N.
=N.
Если A~  , т.е. A={1,2,4,8,…,
, т.е. A={1,2,4,8,…,  ,…}, то множество A называется континуальным (или континуумом). Мощность
,…}, то множество A называется континуальным (или континуумом). Мощность  .
.
Основное правило комбинаторики (показано на примере)
Date: 2015-04-23; view: 699; Нарушение авторских прав