Естественная конвекция

Естественная или свободная конвекция происходит в газах или жидкостях с переменной плотностью в поле массовых сил, например, в поле земного тяготения. При этом возникают силы плавучести (Архимеда). В реальных условиях механизмы естественного и вынужденного переноса тепла могут действовать одновременно. Соотношение между тепловыми потоками, вызванными естественной и вынужденной конвекцией оцениваются отношением сил плавучести пропорциональных ∆ρqh (где ∆ρ - разность плотностей в точках, разделенных расстоянием h, q - ускорение свободного падения) и сил инерции пропорциональных ρU². Это отношение называется числом Ричардсона.

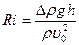
При малых относительных изменениях плотности 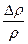по сравнению с характерной величиной 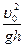преобладает вынужденная конвекция. При условии 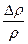> 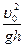процессом, определяющим перенос тепла является естественная конвекция.

Разность плотностей ∆ρ = ρ – ρ₀ выражают через разность температур

,

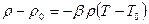где 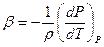- коэффициент термического расширения.

Критерием, определяющим интенсивность теплообмена при естественной конвекции, является число Грасгофа, которое характеризует соотношение сил плавучести и вязкости

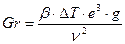
При обработке опытных данных о теплоотдаче при естественной конвекции используется также число Рэлея

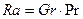
В модели Буссинеска изменение плотности учитывается лишь при определении массовой силы плавучести.

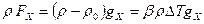(9.1)

где 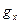- проекция ускорения свободного падения на выбранную ось координат х.

Тогда уравнение плоского движения в проекции на ось х при условии

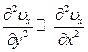
запишется в виде

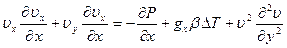(9.2)

Естественная конвекция вблизи твердой стенки в большом объеме обладает свойствами пограничного слоя. Однако поле скорости непосредственно связано с распределением температуры. Рассмотрим ламинарное течение в пристенном слое вблизи нагретой вертикальной пластины в неограниченном пространстве.

Уравнения пограничного слоя для стационарных свободноконвективных течений имеет вид:

- уравнение неразрывности

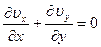(9.3)

- уравнение движения в проекции на ось х

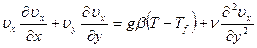(9.4)

- уравнение энергии

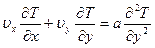(9.5)

Для решения (9.3) – (9.5), следуя Польгаузену, переходит к новым переменным

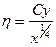
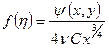
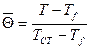(9.6)

где ψ (х,у) - функция тока,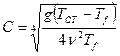

Проекции скорости в этих переменных выражаются следующим образом

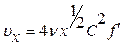
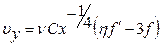(9.7)

Тогда из (9.6), (9.7) получим два обыкновенных дифференциальных уравнения:

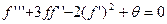
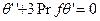(9.8)

Система (9.8) решается при следующих граничных условиях

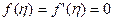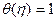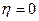
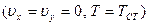
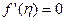
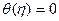, при

при 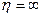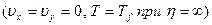(9.9)

Уравнения (9.8) с граничными условиями (9.9) решаются численно или методом интегральных соотношений. Полученное численное решение после перехода к исходным физическим переменным 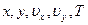определяет локальное число :

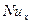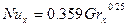(9.10)

и среднее число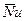

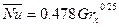(9.11)

где .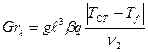

Для расчета теплоотдачи от пластины, установленной с учетом наклона между нижней теплоотдающей поверхностью пластины и вертикалью φ

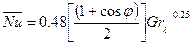(9.12)

где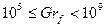

Для обращенной вверх нагретой пластины

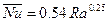(9.13)

где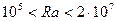

Для турбулентной естественной конвекции установлена критериальная зависимость

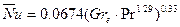(9.14)

где Pr=2.4-118,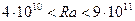

При расчете конвективной теплоотдачи за счет механизма естественной конвекции для вертикальных пластин, горизонтальных и вертикальных цилиндров, шаров применяется формула

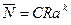(9.15)

где характерный размер для вертикальных пластин и цилиндров – высота, а для горизонтальных цилиндров и шаров – диаметр, физические параметры определяются при 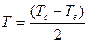, Pr>0.7

Эмпирические константы С и n различные в разных диапазонах по числу Рэлея:

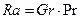(9.16)

- режим псевдотеплопроводности (10^-3<Ra<5∙10²), С = 1, 18,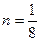

- режим сформировавшегося ламинарного слоя

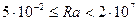С = 0,54;

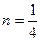
- переходный и турбулентный режим

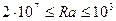С = 0,135;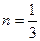

При естественной конвекции в ограниченном пространстве толщина слоя соизмерима с размерами пространства. Поэтому перенос теплоты существенно зависит от формы этого пространства.

В слое жидкости или газа с температурой нижней пластины Т₂ > Т₁, расположенном между двумя плоскими горизонтальными пластинами, отстоящими на расстоянии δ, естественная конвекция возникает при

,

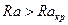где 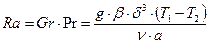- число Рэлея, Ra_кр = 1700. (9.17)

При 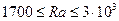возникает ползущее течение с малыми скоростями. Образуются шестигранные в плане ячейки. В опытах с большинством жидкостей отличается подъем жидкости в центрах ячеек и опускание на гранях. В опытах с газами наблюдается обратная картина, что связано с возрастанием вязкости с ростом температуры. Вязкость жидкости снижается с ростом температуры. Критериальное уравнение теплообмена имеет вид

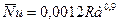(9.18)

где 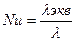, 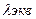- эквивалентная с учетом конвекции теплопроводность.

Режим развитой ламинарной конвекции наблюдается при

, возникает структура чередующихся длинных горизонтальных валов. Число Нуссельта определяется зависимостью

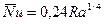
В переходном режиме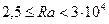

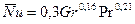(9.19)

При

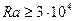
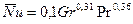(9.20)

В формулах (9.17) – (9.20) в качестве определяющей принята температура

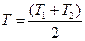, определяющий размер – δ.

Удельный тепловой поток через рассмотренный щелевой зазор δ находится по формуле

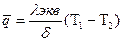(9.21)

где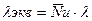

Следует отметить, что численные решения уравнений Навье-Стокса удовлетворительно согласуются с обобщенными экспериментальными данными (9.17) – (9.20).

Рассмотрим конвекцию воздуха в вертикальном щелевом зазоре δ между плоскими пластинами высотой h (h / δ = 10) имеющими температуры Т₁ и Т₂ > Т₁ при 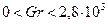интенсивность переноса теплоты определяется коэффициентом теплопроводности. При 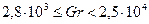наблюдается режим, когда начинает формироваться ламинарное течение. В диапазоне 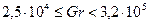появляется режим развитого ламинарного пограничного слоя. Переходный от ламинарного к турбулентному слою характеризуется условием 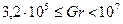. 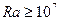При наблюдается развитое турбулентное течение.

Для капельных жидкостей пр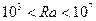и и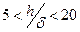

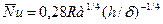(9.22)

Для воздуха при и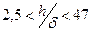

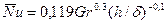(9.23)

В формулах (9.22) и (9.23) характерный размер – ширина щели δ, 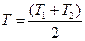, ∆Т = Т₂ – Т₁,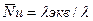

Date: 2015-05-09; view: 1385; Нарушение авторских прав