
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Определение энергетических параметров идеальных газов
|
|
с учетом влияния температуры на cp и cv
Рассчитанные по квантовой теории значения теплоемкостей идеальных газов cpи cv для различных температур позволяют аппроксимировать их зависимость от температуры в степенной полином вида
cp = a + b1t + b2t2 +... + bntn. (4.33)
Таким образом, мы имеем функциональные зависимости cp=F1(t) и cv=F2(t). В принципе достаточно знать функциональную зависимость cp или cv от температуры, поскольку для идеальных газов cp = cv + R. На практике для удобства расчетов в справочных таблицах приводят обе теплоемкости как функции от температуры.
Зная зависимости cp и cv от температуры, можно рассчитать энергетические параметры идеальных газов u, h, s, используя уравнение состояния идеального газа и первый закон термодинамики.
В таблицах термодинамических свойств газов [8] расчет энергетических параметров совмещен с расчетом обратимого адиабатного процесса. Такое совмещение имеет определенную целесообразность, т.к. адиабатный процесс имеет широкое распространение в практике (в компрессорах, газовых турбинах, двигателях внутреннего сгорания и т.п.), кроме того, этот процесс довольно громоздкий в своей расчетной части.
Расчет других процессов идеальных газов также может осуществляться по этим таблицам, но в этом случае определение всех энергетических параметров ведется только по температурам.
Рассмотрим принцип построения таких таблиц и их использование для расчета газовых процессов.
В основу построения этих таблиц положены уравнения первого закона термодинамики для обратимого адиабатного процесса идеального газа:
δq = du + δl = cvdT + Pdv = 0;
δq = dh - vdP = cpdT - vdP = 0.
Поделив эти уравнения на уравнение состояния идеального газа Pv=RT, получим соотношения
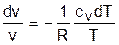 ; (4.34)
; (4.34)
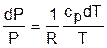 . (4.35)
. (4.35)
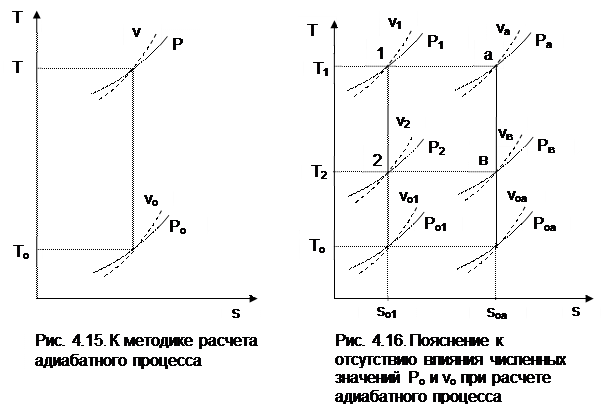
Зафиксировав начало адиабатного процесса в виде точки с постоянными параметрами Ро, Tо, vо, проинтегрируем эти выражения от точки на адиабатном процессе с температурой То до точки с температурой Т и соответствующими ей давлением и объемом Р и v (рис.4.15). В результате интегрирования получим выражения
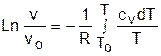 ; (4.36)
; (4.36)
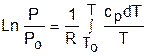 . (4.37)
. (4.37)
Введем понятия относительного объема qo и относительного давления po:
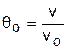 ; (4.38)
; (4.38)
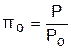 . (4.39)
. (4.39)
Для адиабатного процесса 12 (рис.4.16) с параметрами в начальной точке Р1, T1 и v1 и в конечной точке Р2, T2 и v2 относительные объемы и давления будут рассчитываться в соответствии с уравнениями (4.35) и (4.36) по формулам
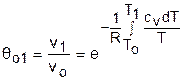 ;
; 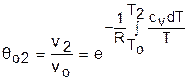 ;
;
 |
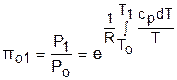 ;
; 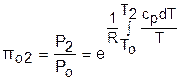 .
.
Из этих формул следует, что для адиабатного процесса справедливы соотношения
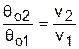 ; (4.40)
; (4.40)
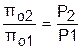 . (4.41)
. (4.41)
Величины относительных объемов и давлений есть функции одного параметра – температуры, поскольку То мы приняли в виде постоянной величины, а сp и сv являются функциями температуры. При этом численные значения величин Рo и vо никакой роли не играют, поскольку в расчетах адиабатного процесса нас интересуют относительные давления и объемы, а они зависят только от То и Т.
Для наглядности этого утверждения на рис.4.16 показаны два адиабатных процесса, проходящих в одном и том же интервале температур Т1 – Т2. Приняв для этих адиабат одинаковую температуру То, можно записать следующие соотношения:
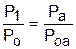 ,
, 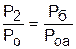 ,
, 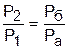 ;
;
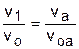 ,
, 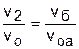 ,
, 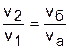 .
.
Из этих соотношений видно, что несоответствие энтропии so1 адиабатного процесса 12 с энтропией soа процесса ав, т.е. различие в численных значениях давлений и объемов в этих процессах при То, не влияет на отношение давлений и объемов в этих процессах, и если они проходят в одинаковых интервалах температур, то и отношения давлений и объемов будут одинаковы.
Это объясняется тем, что все изобары и изохоры идеальных газов в Т,s- диаграмме – эквидистантные кривые. Характер изобары в Т,s- диаграмме определяет теплоемкость сp, а изохоры – сv, и при одинаковых температурах на всех изобарах и изохорах одинаковые теплоемкости.
Таким образом, для адиабатного процесса по po1 и qo1 всегда можно определить соответствующую им температуру Т1 и теплоемкости сp1 и сv1. В свою очередь, зная параметры начальной точки этого процесса и степень повышения давления р2/р1 или степень сжатия v1/v2, можно определить параметры конца процесса, найдя p02=p01(p2/p1) или q02=q01(v2/v1), а по ним определить температуру Т2 и рассчитать весь адиабатный процесс.
В таблицах [12] в качестве То для расчета po и qo принято значение температуры абсолютного нуля. В принципе можно брать любое То, а Ро и vо вообще роли не играют (см. приведенный выше анализ).
Для определения внутренней энергии и энтальпии газов принимают начало отсчета внутренней энергии uo=0 при Тo. В качестве То в таблицах [8] принят абсолютный нуль, То=0 К. Расчет u и h ведется по формулам идеальных газов:
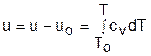 ; (4.42)
; (4.42)
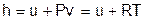 . (4.43)
. (4.43)
При этом в нашем случае начала отсчета внутренней энергии и энтальпии совпадают и равны нулю, т.к. То= 0 К. Энтальпия может быть рассчитана аналогично внутренней энергии интегрированием, при этом используется функциональная зависимость теплоемкости сp от температуры:
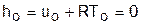 ;
;
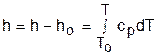 . (4.44)
. (4.44)
Поскольку u и h являются функциями температуры, они могут быть определены и через qo и po.
Для расчета изменения энтропии используется первый закон термодинамики для обратимых процессов идеальных газов:
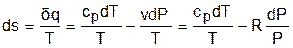 .
.
Интегрируя это выражение для двух состояний идеального газа, получим формулу для расчета разности энтропий:
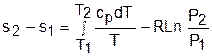 . (4.45)
. (4.45)
Интегральное слагаемое выражения (4.45) можно представить в виде разности:
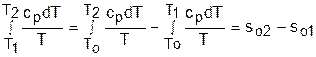 . (4.46)
. (4.46)
Величины, входящие в эту разность, могут восприниматься как изменение энтропии в зависимости от температуры. Они обозначаются как sо1 и sо2 и могут быть рассчитаны при фиксации То для каждой температуры. Величина so является функцией температуры, а для адиабатного процесса – функцией po и qo. В таблицах [12] so рассчитано при То=0 К. Используя табличные значения so, можно определить разницу энтропий в точках по формуле
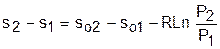 . (4.47)
. (4.47)
Если требуется абсолютное значение энтропии, необходимо выбрать начало ее отсчета (sо=0) при То и Ро. В качестве То и Ро могут быть приняты любые величины. В случае выбора То=0 К, как и в таблицах [12], получим расчетное выражение абсолютной энтропии, например, для точки с Р1 и Т1:
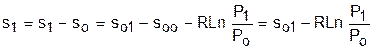 , (4.48)
, (4.48)
где  ,
, 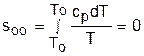 .
.
При несоответствии То значению абсолютного нуля для определения sо1 и абсолютной энтропии s1 в выражении (4.48) появится дополнительное постоянное вычитаемое
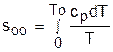 , (4.49)
, (4.49)
которое уменьшит абсолютное значение энтропии s1, но не скажется на величине изменения энтропии s2-s1. То есть значение температуры, принятое для начала отсчета абсолютной энтропии, не обязательно должно соответствовать базовой температуре То, принятой для расчета табличных величин sо. Также произволен и выбор значения Ро для расчета абсолютного значения энтропии.
Величины cp, cv, u, h, so, po, qo, рассчитанные по формулам (4.32) – (4.45) для различных газов, сводятся в специальные таблицы [12] термодинамических свойств газов. В этих таблицах приводятся величины cp, cv, u, h, so, po, qo – в зависимости от температуры. Для расчета адиабатного процесса можно пользоваться всеми приведенными в таблице величинами. Для расчетов других процессов можно пользоваться только величинами cp, cv, u, h, so как функциями от температуры.
Приведем пример использования этих таблиц для расчетов процессов газов, подчиняющихся уравнению Pv=RT.
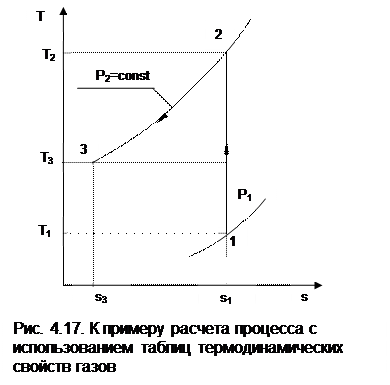
Пусть требуется рассчитать обратимый адиабатный процесс сжатия воздуха от состояния Р1=1 бар и t1=17 оС до давления Р2=10 бар, а затем рассчитать количество теплоты и изменение энтропии при охлаждении воздуха при постоянном давлении Р2=const от t2 до t3=20 оС (рис.4.17).
Решение
По таблицам термодинамических свойств воздуха [9, 12] определяем p01 по известной температуре t1=17 oC. Определив p01=1,2339, рассчитываем p02 по известному отношению давлений адиабатного процесса:
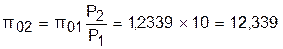 .
.
 |
По величине p02 определяем по таблицам [9, 12] температуру в конце адиабатного процесса: t2 = 283 oC (взято с точностью до 1о). Зная температуры во всех трех точках сложного процесса, определим по ним из таблиц необходимые для расчета энергетические параметры: h1=290,28 кДж/кг, u1=207,01 кДж/кг, h2=561,13 кДж/кг, u2=401,52 кДж/кг, h3=293,29 кДж/кг, u3=209,16 кДж/кг.
Для адиабатного процесса 12 определим:
h2 - h1 = 561,13 - 290,28 = 270,85 кДж/кг,
u2 - u1 = - l = 401,52 - 207,01 = 199,51 кДж/кг.
Для изобарного процесса 23 количество теплоты рассчитывается как разница его энтальпий:
q23 = h3 - h2 = 293,29 - 561,13 = - 267,84 кДж/кг.
Для определения изменения энтропии в процессе 23 из таблиц по t2 и t3 возьмем sо2=7,3298 кДж/(кг·К) и sо3=6,6789 кДж/(кг·К) и рассчитаем изменение энтропии:
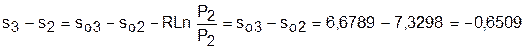
 .
.
Изменение энтропии происходит только за счет изменения температуры, т.к. процесс 23 – изобарный.
Для определения абсолютных значений энтропий необходимо задаться величиной Ро. Приняв Ро=1 бар, рассчитаем s1, s2 и s3:

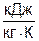 ;
;
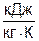 ,
,
т.к. в пределах погрешности расчетов s1=s2, то это подтверждает, что процесс 12 адиабатный.
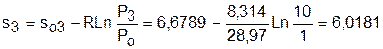
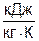 .
.
Проверим ранее полученное значение разности энтропий s3-s2 по разности абсолютных энтропий в этих точках:
s3 - s2 = 6,0181 - 6,6689 = - 0,6508 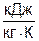 .
.
В этом случае сходимость результатов тоже очевидна.
Date: 2015-05-09; view: 991; Нарушение авторских прав